1)
Gọi O là tâm đa giác đáy (tâm hình vuông)
a) V(S.ABCD) = $\frac{1}{3}\frac{a\sqrt{6}}{2}.a^2$
b)
Ta tính được SK = $\sqrt {OK^2 + OS^2} = (\frac{a}{2})^2 + \frac{a\sqrt{6}}{2}^2) $
Và tính được d(O, (SDM)) = $\frac{OS.OK}{SK}$
Mà 2d (O, (SDM)) = d(B,(SDM))
Ta cũng tính được d (S, DC) = SK => d(N, DC) = $\frac{1}{2}SK$ (vì N là trung điểm SC)
Tổng hợp lại thì V(B.CMN) = $\frac{1}{3}.d(B,(SDM)).\frac{1}{2}.d(N, DC).CM$
c)
Như vậy chỉ cần tính thêm S(M.DPQ) là được
Ta cần đi xác định tỉ lệ SP/SD, chính xác là PD/SD để suy ra được d(P;(ABCD)) hay d(P, (DQM))
Có một sự thật là theo định lý Menelaus thì (đã xét dấu): $\frac{PS}{PD}. \frac{MD}{MC} . \frac{NC}{NS} = 1$ =>$ \frac{PS}{PD} = \frac{1}{2}$
=> $\frac{BD}{SD} = \frac{2}{3}$ (1)
Diện tích tam giác DMQ ta nhờ hình vẽ sau:
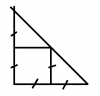
Như vậy S(DMQ) = $\frac{1}{2}(2a)^2$
Từ (1) ta tính được d(P,(ABCD)) = $\frac{2}{3}SO$
Từ đó ta tính được V(P.QDM) = $\frac{1}{3}.\frac{2}{3}SO.S_{DMQ}$
Từ đó V cần tìm = V(P.QDM) - P(B.CMN)
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
