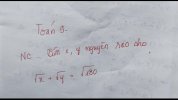[math]\sqrt{x}+\sqrt{y}=\sqrt{180} (*)[/math][math]\textnormal{Điều kiện:} x,y\ge 0[/math][math]\textnormal{Có:} \sqrt{x}+\sqrt{y}=\sqrt{180}[/math][math]=>\sqrt{y}=\sqrt{180}-\sqrt{x}[/math][math]=>\sqrt{y}^2=(\sqrt{180}-\sqrt{x})^2[/math][math]=>y=180-2\sqrt{180x}+x[/math][math]\textnormal{Vì x,y là số nguyên nên:} \sqrt{180x} \textnormal{là số nguyên.}[/math][math]=>6\sqrt{5x} \textnormal{là số nguyên.}[/math][math]=>\sqrt{5x} \textnormal{là số nguyên.}[/math][math]\textnormal{Chứng minh tương tự, ta có:} \sqrt{5y} \textnormal{là số nguyên.}[/math][math]\textnormal{Đặt} x=5a^2, y=5b^2 (a,b\in \Z).[/math][math]\textnormal{Thay} x=5a^2,y=5b^2 \textnormal{vào phương trình (*), ta được:}[/math][math]\sqrt{5a^2}+\sqrt{5b^2}=\sqrt{180}[/math][math]=>\sqrt{5}a+\sqrt{5}b=6\sqrt{5}[/math][math]=>a+b=6 [/math][math] \textnormal{Lập bảng giá trị như sau:} [/math][math]\def\arraystretch{1.5} \begin{array}{c:c:c:c:c:c:c:c} a & 0 & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline b & 6 & 5 & 4 & 3 & 2 & 1 & 0 \\ \hline x=5a^2 & 0 & 5 & 20 & 45 & 80 & 125 & 180 \\ \hline y=5b^2 & 180 & 125 & 80 & 45 & 20 & 5 & 0 \end{array}[/math][math]\textnormal{Vậy phương trình có nghiệm nguyên (x,y)} \in \lbrace\textnormal{(0,180),(5,125),(20,80),(45,45),(80,20),(125,5),(180,0)}\rbrace.[/math]Chúc mừng năm mới!
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
