[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
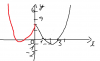
Cho hàm số y=x^2-4+3 có đồ thị như hình vẽ dưới đây
Đặt f(x) = x^2-4[tex]\left | x \right |[/tex]+3, gọi S là tập hợp các giá trị nguyên của tham số m để phương trình [tex]\left | f(x) \right |[/tex]=m có 8 nghiệm phân biệt. Số phần tử của S bằng bao nhiêu
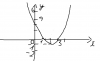
Cho mk xin luôn phương pháp làm dạng giải 8 nghiệm, 4 nghiệm, 3 nghiệm được không ạ?
Hàm số vẽ xấu mn thông cảm ạ
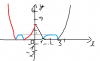
Đặt f(x) = x^2-4[tex]\left | x \right |[/tex]+3, gọi S là tập hợp các giá trị nguyên của tham số m để phương trình [tex]\left | f(x) \right |[/tex]=m có 8 nghiệm phân biệt. Số phần tử của S bằng bao nhiêu

Cho mk xin luôn phương pháp làm dạng giải 8 nghiệm, 4 nghiệm, 3 nghiệm được không ạ?
Hàm số vẽ xấu mn thông cảm ạ