Đề ra :
Trên mặt nước có A, B là hai nguồn đồng bộ. C, D là hai điểm trên mặt nước sao cho ABCD là hình vuông. Biết trên CD chỉ có 7 điểm dao động với biên độ lớn nhất . Tìm số điểm dao động cực đại ít nhất và nhiều nhất trên AB.
GIẢI:
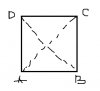
* Gọi cạnh của hình vuông là [tex]d[/tex].
* Theo đề thì số cực đại trên [tex]CD[/tex] chỉ có [tex]07[/tex]. Suy ra có hai trường hợp xảy ra với bậc tại [tex]C[/tex] và tại [tex]D[/tex]
- Trường hợp 01: [tex]k_D=3;k_C=-3[/tex], tương ứng với [tex]\lambda_{max}[/tex]
- Trường hợp 02: [tex]k_D=3,999;k_C=-3,999[/tex], tương ứng với [tex]\lambda_{min}[/tex]
* Vì là hình vuông nên [tex]04[/tex] cạnh bằng nhau. Cạnh huyền [tex]DB=AC=d\sqrt{2}[/tex]
* Giải trường hợp 01: [tex]d_2-d_1=k_D \lambda_{max}<=>d\sqrt{2}-d=3.\lambda_{max}=>\lambda_{max}=\frac{d(\sqrt{2}-1)}{3}[/tex]
* Giải trường hợp 02: [tex]\lambda_{min}=\frac{d(\sqrt{2}-1)}{3,999}[/tex]
a) Số cực đại nhiều nhất trên [tex]AB[/tex] tương ứng với bước sóng bé nhất
Áp dụng
công thức tính cực đại trên đoạn nối hai nguồn, ta tính được: [tex]-\frac{AB}{\lambda}\leq k\leq \frac{AB}{\lambda}[/tex]
thì ta có: [tex]-\frac{d}{\frac{d(\sqrt{2}-1)}{3,999}}\leq k\leq \frac{d}{\frac{d(\sqrt{2}-1)}{3,999}}<=>-9,65\leq k\leq 9,65[/tex]
Vậy trên [tex]AB[/tex] có nhiều nhất là [tex]19[/tex] cực đại
b) Tương tự như trên, số cực đại ít nhất tương ứng với [tex]\lambda_{max}[/tex]
[tex]-\frac{AB}{\lambda}\leq k \leq \frac{AB}{\lambda}[/tex]
thì [tex]-7,24\leq k\leq 7,24[/tex]
Vậy trên [tex]AB[/tex] có ít nhất [tex]15[/tex] cực đại
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
