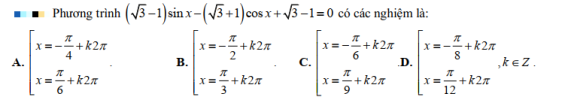[imath]( \sqrt{3}-1) \sin{x} - ( \sqrt{3}+1) \cos{x} +\sqrt{3}-1=0[/imath]
[imath]\Leftrightarrow ( \sqrt{3}-1) \sin{x} - ( \sqrt{3}+1) \cos{x} =1-\sqrt{3}[/imath]
[imath]\Leftrightarrow \dfrac{ \sqrt{3}-1}{ \sqrt{( \sqrt{3}-1)^2+( \sqrt{3}+1)^2}} \sin{x} - \dfrac{ \sqrt{3}+1}{ \sqrt{( \sqrt{3}-1)^2+( \sqrt{3}+1)^2}} \cos{x} = \dfrac{ 1-\sqrt{3}}{ \sqrt{( \sqrt{3}-1)^2+( \sqrt{3}+1)^2}}[/imath]
[imath]\Leftrightarrow \dfrac{ \sqrt{6} - \sqrt{2}}{4} \sin{x} - \dfrac{ \sqrt{6} + \sqrt{2}}{4} \cos{x} = \dfrac{- \sqrt{6}+ \sqrt{2}}{4}[/imath]
[imath]\Leftrightarrow \sin{x} \cos{\dfrac{5 \pi}{12}} - \cos{x} \sin{\dfrac{5 \pi}{12}}= \dfrac{- \sqrt{6}+ \sqrt{2}}{4}[/imath]
[imath]\Leftrightarrow \sin{ \left (x - \dfrac{5 \pi}{12} \right )}= \dfrac{- \sqrt{6}+ \sqrt{2}}{4}[/imath]
[imath]\Leftrightarrow \sin{ \left (x - \dfrac{5 \pi}{12} \right )}= \sin{ \left ( - \dfrac{ \pi}{12} \right )}[/imath]
[imath]\Leftrightarrow
\left[\begin{matrix}
x - \dfrac{5 \pi}{12} = - \dfrac{ \pi}{12} + k2 \pi \\ \\
x - \dfrac{5 \pi}{12} = \pi - \left (- \dfrac{ \pi}{12} \right ) +k2 \pi
\end{matrix}\right.
[/imath]
[imath]\Leftrightarrow
\left[\begin{matrix}
x = \dfrac{ \pi}{3} + k2 \pi \\ \\
x = \dfrac{3 \pi}{2} +k2 \pi
\end{matrix}\right. \ \ (k \in \mathbb{Z})
[/imath]
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
