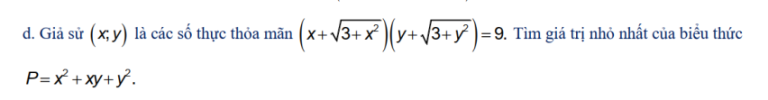Toán 9 Tìm Min

[Nguyễn Chi Xuyên]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

giúp mình câu này với ạ

 

[2712-0-3]

View attachment 219831
giúp mình câu này với ạ

Nguyễn Chi XuyênTrước hết ta phải giải được giả thiết, khá quen thui.
Ta có: $\dfrac{9}{y+\sqrt{3+y^2}} = \sqrt{3+y^2} -y$
Suy ra $x+\sqrt{3+x^2} = 3\sqrt{3+y^2} - 3y \Rightarrow x+3y =3\sqrt{3+y^2}- \sqrt{3+x^2}$
Tương tự ta có: $3x+y =3\sqrt{3+x^2}- \sqrt{3+y^2} \Rightarrow \sqrt{3+y^2} = 3\sqrt{3+x^2} - 3x-y$.
Thay vào biểu thức trên ta có:
$x+3y =9\sqrt{3+x^2} - 9x-3y -\sqrt{3+x^2} \Rightarrow 10x + 6y = 8\sqrt{3+x^2} \Rightarrow 5x+3y = 4\sqrt{3+x^2}$
$\Rightarrow 25x^2 +30xy + 9y^2 = 16x^2 + 48 \Rightarrow 9x^2 + 30xy+9y^2 = 48 \Rightarrow 3x^2+10xy+3y^2 = 16$
Ta có: $16P = 16x^2+16xy+16y^2 = 3(3x^2+10xy+3y^2) + 7(x^2+y^2-2xy)=48 +7(x-y)^2 \geq 48 \Rightarrow P\geq 3$.
Dấu bằng xảy ra khi $x=y=1$