- 23 Tháng ba 2018
- 1,367
- 1,923
- 241
- 21
- Thanh Hóa
- Trường THPT Triệu Sơn 4
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
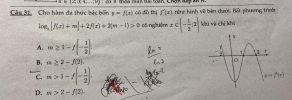
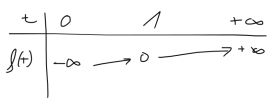
Cho hàm đa thức bậc bốn [imath]y = f(x)[/imath] có đồ thị [imath]f'(x)[/imath] như hình vẽ bên dưới . Bất phương trình [imath]\log_2\left[f(x) + m\right] + 2f(x) + 2(m-1) > 0[/imath] có nghiệm [imath]x \in \left(-\dfrac{1}2 ; 2 \right)[/imath]
Giúp em câu này với ạ @Cáp Ngọc Bảo Phương @vangiang124
Giúp em câu này với ạ @Cáp Ngọc Bảo Phương @vangiang124
Attachments
Last edited by a moderator: