tìm diện tích tam giác khi cho (p) và (d) cắt nhau

[khoangkhackidieu]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

giúp mik với nha, thanks các bạn đã đọc và giải giúp mik
p/s : chỉ cần giúp mik câu c thôi. à nhưng mà làm ơn vẽ hình ra luôn để mik biết đâu là điểm A , đâu là điểm B nha

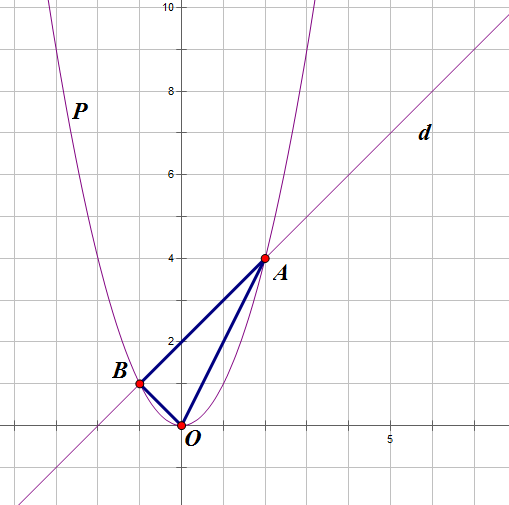
Cho y = [TEX] X^2[/TEX] (P) và đường thẳng y = X + 2 (d)
a/ vẻ (P) và (d)
b/ Tình tọa độ giao điểm A,B của (P) và (d)
c/ tính diện tích tam giác OAB

 

[buivanbao123]

b)Toạ độ giao điểm A,B là $x^{2}=x+2$
\Leftrightarrow $x^{2}-x-2$=0
\Leftrightarrow x=2 hoặc x=-1
Ta có: x=2 \Rightarrow y=4
x=-1 \Rightarrow y=4
Vậy toạ độ A(2,4),B(-1,4)

 

[khoangkhackidieu]

thanks bạn nha , vậy bạn có thể giải câu C đc ko ? mik chỉ tìm đc đoạn OA và OB . tuy nhiên không biết chưng minh nó là tam giác vuông nên đang bí , hì

 

[buivanbao123]

Câu a anh lười vẽ quá anh chỉ hướng dẫn
để vẽ đồ thị y=$x^{2}$ ta chọn ngẫu nhiên một đại lượng x thế vào sẽ tìm được y,(P) là một đường cong hướng lên trên do a>0
Để vẽ đồ thị y=x+2 đường thẳng đi qua A(0,2) và B(-2,0) đường thẳng cắt 2 trục Ox,Oy

 

[demon311]

c)

Xác định khoảng cách giữa các điểm O,A,B rồi dùng Pitago chứng minh tam giác vuông tại B (theo hình) rồi tìm S dễ dàng

 

[demon311]

Công thức khoảng cách giữa 2 điểm của lớp 10 (bồi dưỡng lớp 9 hoặc CASIO có nhắc đến):
$A(x_A;y_A) \; ; \; B(x_B;y_B) \\
AB=\sqrt{ (x_A-x_B)^2+(y_A-y_B)^2}$

 

[buivanbao123]

c)Căn cứ vào toạ độ điểm A,B \Rightarrow AB vuông góc Ox tại điểm H
Sabc=$\dfrac{1}{2}.AB.OH$=$\dfrac{1}{2}.4.3$=6

 

[demon311]

Câu a anh lười vẽ quá anh chỉ hướng dẫn
để vẽ đồ thị y=$x^{2}$ ta chọn ngẫu nhiên một đại lượng x thế vào sẽ tìm được y,(P) là một đường cong hướng lên trên do a>0
Để vẽ đồ thị y=x+2 đường thẳng đi qua A(0,2) và B(-2,0) đường thẳng này đi qua gốc toạ độ

Bác nhầm với ptdt lớp 10 rồi
$ax+by+c=0 $ có $c=0$ mới đi qua gốc toạ độ nhé
Còn ở đây hệ số tự do là 2

 

[khoangkhackidieu]

theo e thì chứng minh sao mà AB vuông góc với OB ạ , thì tính đc cạnh AB. rồi tính đc S ạ
hoặc tính đc cạnh AB và chứng minh bình phương của AB bằng tổng bình phương của OA và OB theo pytago , n e lại bí chổ tính AB vs chứng minh vương góc

 

[demon311]

Thì anh cho công thức rồi mà, em có toạn đọ cả 3 đỉnh, thì dễ dàng tính khoảng cách giữa chúng. Xong rồi như cái hình của anh thì $AB \perp OB$, nên em cần chưng minh là $AB^2+OB^2=OA^2$
Thế thôi
Có mỗi AB em tính S kiểu gì
Mà may mà bài này họ cho vuông góc đó

 

[eye_smile]

c, $A(x_1;y_1);B(x_2;y_2)$ \Rightarrow $x_1;x_2$ là 2 nghiệm của PT:
${x^2}=x+2$
\Leftrightarrow ${x^2}-x-2=0$
\Rightarrow $A(-1;1);B(2;4)$

\Rightarrow ${OA^2}={2^2}+{4^2}=20$
${OB^2}=1+1=2$
${AB^2}={(2+1)^2}+{(4-1)^2}=18$

\Rightarrow ${OB^2}+{AB^2}={OA^2}$

\Rightarrow tam giác OAB vuông tại B

\Rightarrow $S=\dfrac{1}{2}.OB.AB=...$

 

[demon311]

Anh đoán khoanhkhackidieu giải sai vì Bảo giải nhầm nghiệm do ngộ nhận hệ số tự do = 0

 

[khoangkhackidieu]

e tìm được toạ độ của 3 điểm rồi , tuy nhiên làm s mà tìm ra AB để chứng minh nó là tam giác vuông ạ , e đang bí chỗ chứng minh tam giác vuông, nếu theo như anh DEMON311 thì tự nhận nó là tam giác vuông mất rồi

 

[eye_smile]

c, $A(x_1;y_1);B(x_2;y_2)$ \Rightarrow $x_1;x_2$ là 2 nghiệm của PT:
${x^2}=x+2$
\Leftrightarrow ${x^2}-x-2=0$
\Rightarrow $A(-1;1);B(2;4)$

\Rightarrow ${OA^2}={2^2}+{4^2}=20$
${OB^2}=1+1=2$
${AB^2}={(2+1)^2}+{(4-1)^2}=18$

\Rightarrow ${OB^2}+{AB^2}={OA^2}$

\Rightarrow tam giác OAB vuông tại B

\Rightarrow $S=\dfrac{1}{2}.OB.AB=...$

Mình đã c/m theo Pytagore đảo rồi mà bạn...................................

 

[demon311]

e tìm được toạ độ của 3 điểm rồi , tuy nhiên làm s mà tìm ra AB để chứng minh nó là tam giác vuông ạ , e đang bí chỗ chứng minh tam giác vuông, nếu theo như anh DEMON311 thì tự nhận nó là tam giác vuông mất rồi

Anh có nhận gì đâu em
Anh chỉ nói là em có đọ dài 3 cạnh thì dùng Pitago mà chứng minh nó vuông góc nhé