Toán 9 Tìm điểm cố định

[nguyenduykhanhxt]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Giúp mình lm câu b

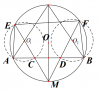
Cho (O) dây AB cố định không đi qua O. M là điểm chính giữa của cung nhỏ AB; C và D là các điểm phân biệt nằm giữa A và B. Các đường thẳng MC và MD cắt đường tròn tâm (O) tại E và F.
a) Chứng minh rằng C, D, E, F nằm trên một đường tròn
b) Gọi O1 , O2 tương ứng là tâm các đường tròn ngoại tiếp các tam giác ACE và BDF. Chứng minh khi C, D thay đổi trên đoạn AB, các đường thẳng AO1 và BO2 luôn cắt nhau tại một điểm cố định
@Mộc Nhãn ,@TranPhuong27 ,@Hanhh Mingg

 

[Hanhh Mingg]

Kẻ $O_{1}H\perp AC$
ta có tam giác $AO_{1}C$ cân tại $O_{1}$ nên $\widehat{AO_{1}H} =\frac{1}{2}\widehat{AO_{1}C}$
lại có : $\widehat{AEC}=\frac{1}{2}\widehat{AO_{1}C}$
do đó: $\widehat{AEC}=\widehat{AO_{1}H}$ mà $\widehat{AEC}=\widehat{MAB}\Rightarrow \widehat{MAB}=\widehat{AO_{1}H}$
Vì tam giác $AO_{1}H$ vuông tại H nên $\widehat{O_{1}AH}+\widehat{AO_{1}H}$ =90 mà $\widehat{MAB}=\widehat{AO_{1}H}$
$\Rightarrow \widehat{O_{1}AH}+\widehat{MAB}$ =90 $\Rightarrow \widehat{O_{1}AM}$ =90 nên MA là tiếp tuyến tại A của đt ($O_{1}$)
$\Rightarrow O_{1}A\perp MA$
Do đó nếu kéo dài $O_{1} A$ cắt đt (O) tại N thì M,O,N thẳng hàng mà M cố định nên N cố định
CMTT ta có: MB cũng là tiếp tuyến của đt ($O_{2}$) nên $O_{2} B$
cũng đi qua N
Vậy ta có đpcm.