- 30 Tháng bảy 2021
- 490
- 466
- 76
- 19
- Quảng Nam
- THPT chuyên Lê Thánh Tông
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Dạ cho mình hỏi là bài này sách bài tập làm thiếu đúng không ạ?
Tìm cấp số cộng $(u_n)$ biết:
$\begin{cases}u_1+u_2+u_3=27\\u_1^2+u_2^2+u_3^2=275\end{cases}$
Mình đọc mãi mà không hiểu làm sao sách suy ra được dãy tăng, mình thấy nếu đổi u1 và u3 thì vẫn thoả mãn ạ.
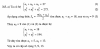
Mình cảm ơn.
Tìm cấp số cộng $(u_n)$ biết:
$\begin{cases}u_1+u_2+u_3=27\\u_1^2+u_2^2+u_3^2=275\end{cases}$
Mình đọc mãi mà không hiểu làm sao sách suy ra được dãy tăng, mình thấy nếu đổi u1 và u3 thì vẫn thoả mãn ạ.
Mình cảm ơn.
Attachments
Last edited by a moderator:

