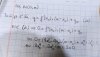Chị đưa ra cho em phương pháp làm bài này nhé. Chứ làm theo cách của em thì bài này không ra được
Phương pháp chị đưa ra là phương pháp chung để giải các bài toán có tiếp tuyến đi qua điểm
Bài toán: Cho hàm số $y=f(x)$ có đồ thị $(C)$ . Viết phương trình tiếp tuyến của $(C)$ đi qua điểm [tex]M(x_{o};y_{o})[/tex]
Cách giải:
Bước 1: Gọi phương trình tiếp tuyến $(d)$ đi qua [tex]M(x_{o};y_{o})[/tex] có hệ số góc $K$ là [tex]y=K(x-x_{o})+y_{o}[/tex]
Bước 2: Điều kiện của $(d)$ là tiếp tuyến của $(C)$
[tex]\left\{\begin{matrix} f(x)=K(x-x_{o})+y_{o} &(1) \\ f'(x)=K & (2) \end{matrix}\right.[/tex]
Giải thích: Phương trình $(1)$ chính là phương trình hoành độ giao điểm của $y=f(x)$ và đường thẳng $(d)$ ( phương trình này phải có nghiệm). Phương trình $(2)$ là đạo hàm 2 vế của phương trình $(1)$
Bước 3: Thay $(2)$ vào $(1)$ ta được [tex]f(x)=f'(x).(x-x_{o})+y_{o}(\ast )[/tex]
Giải [tex](\ast )[/tex] [tex]\rightarrow x=?\overset{(2)}{\rightarrow}K=?\rightarrow pt(d)[/tex]
Em xem xong cái này là sẽ hiểu bài chị làm nhé

 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.