Toán 12 Thể tích

[Nguyễn Ngọc Diệp 565]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

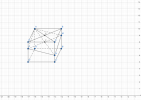
1)Cho hình lập phương (ABCD.A'B'C'D' ). 1 mặt phẳng alpha đi qua A cắt BB', CC', DD' lần lượt tại các điểm M, N,P Tìm tỉ số CN/CC' để alpha chia hình lập phương thành 2 phần và phần chứa đỉnh A có thể tishc bằng 1/2 phần còn lại​

3) Cho hình lập phương ABCD.A'B'C'D' có cạnh 3a. Tính VACB'D'
Nhờ mng giúp mình với ạ

 

[MuHaiW]

Bài 1:
[imath]VABCD.MNP = \dfrac{1}{3} VABCD.A'B'C'D' = \dfrac{1}{3}V[/imath]
[imath]VABCD.MNP= VA.DCNP+VA.BMCN[/imath]
Đặt [imath]\dfrac{CN}{CC'}=x[/imath]
[imath]VABCD.MNP= \dfrac{1}{2}.\dfrac{2}{3}.\dfrac{1}{2}.(\dfrac{DP}{DD'}+x)V+\dfrac{1}{2}.\dfrac{2}{3}.\dfrac{1}{2}(\dfrac{BM}{BB'}+x)V[/imath] (*)
Gọi E là tâm hình vuông ABCD; F là tâm hbh AMNP. Ta dễ dàng chứng minh [imath]CN=DP+BM(=2EF)[/imath]
[imath](*)=\dfrac{1}{2}xV=\dfrac{1}{3}V \rightarrow x=\dfrac{2}{3}[/imath]
Bài 2:
[imath]V C.AB'D'= V- VB'.ABC-VC.B'D'C'-VD'.ADC-VA.A'B'D'[/imath]
[imath]V C.AB'D'= V-4VA.A'B'D'=V-4.\dfrac{1}{6}V=\dfrac{1}{3}V[/imath]
Bạn tham khảo nhé. Chúc bạn học tốt!!!