Toán 12 Thể Tích Khối Đa Diện

[Quyên Trương]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Cho khối chóp S.ABCD có đáy là hình bình hành, thể tích bằng 1. Gọi M là trung điểm cạnh SA; các điểm E,F lần lượt là điểm đối xứng của A qua B và D. Mặt phẳng (MEF) cắt các cạnh SB,SD lần lượt tại các điểm N,P. Thể tích của khối đa diện ABCDMNP bằng

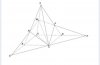
Cách 1: Ta có ΔSAE; ΔSAF có N, P là trọng tâm vì nằm trên giao điểm của 2 đường trung tuyến.
Vì vậy SN/SB = SP/SD = 2/3 và C thuộc EF.
Ta có V(S.MNC) = SM/SA * SN/SB * V(S.ABC) = 1/2 * 2/3 * 1/2 * V(S.ABCD) = 1/6
V(S.MPC) = SM/SA * SP/SD * V(S.ADC) = 1/2 * 2/3 * 1/2 * V(S.ABCD) = 1/6
Vì vậy V(S.MNCP) = V(S.MNC) + V(S.MPC) = 1/6 + 1/6 = 1/3
và V(ABCD.MNP) = V(S.ABCD) - V(S.MNCP) = 1 - 1/3 = 2/3
Cách 2: Dùng công thức tính nhanh tỉ số thể tích
Có x = SM/SA = 1/2; y = SN/SB = 2/3; z = SC/SC = 1; t = SP/SD = 2/3
Vì vậy V(S.MNCP) = xyzt/4 * (1/x + 1/y + 1/z + 1/t) * V(S.ABCD) = 1/3
Mọi người xem và giải thích giùm em mấy chỗ in đậm với ạ. Em cám ơn.

 

[ngocdodo.pp_HM]

Chào em,
+ Em chứng minh tam giác BEC= tam giác DCF, từ đó chứng minh góc BCE+BCD+DCF = 180 độ => 3 điểm E,C,F thẳng hàng
+ Ta có DT tam giác ABC = DT tam giác ACD = 1/2. DT hbh ABCD
=> V(S.ABC)=V(S.ADC)=1/2.V(S.ABCD)
+ Cách 2 là dùng công thức tỷ lệ thể tích, em tách V(S.MNCP) thành 2 khối = V(S.CMN)+V(S.MPC)
Sau đó áp dụng V(S.CMN)/V(S.CAB)= SM/SA.SN/SB.SC/SC = x.y.z
V(S.MPC)/V(S.ADC) = SM/SA.SP/SD.SC/SC=x.z.t
Mà V(S.ABC)=V(S.ADC)=1/2.V(S.ABCD)
=> V(S.MNCP) = xyz.1/2.V(S.ABCD)+xzt.1/2.V(S.ABCD)
Trong đó: x = SM/SA = 1/2; y = SN/SB = 2/3; z = SC/SC = 1; t = SP/SD = 2/3, V(S.ABCD)=1
=> V(S.MNCP) = 1/2.2/3.1/2+1/2.1.2/3.1 = 1/6+1/6=1/3 em nhé!