- 24 Tháng mười 2018
- 1,616
- 1,346
- 216
- 25
- TP Hồ Chí Minh
- Đại học Sư phạm Kỹ thuật TP Hồ Chí Minh
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
1. Lý thuyết về thể tích khối đa diện
- thể tích khối đa diện là thể tích phần không gian mà hình đa diện chiếm, kể cả hình đa diện đó.
- nếu gọi khối đa diện là (H), người ta chứng minh được rằng: thể tích của khối đa diện luôn dương, tức là [tex]V_{(H)}>0[/tex]
- tính chất của thể tích khối đa diện:
+ nếu (H) là khối lập phương có cạnh bằng 1 thì [tex]V_{(H)}=1[/tex]
+ nếu 2 khối đa diện [tex](H_1)[/tex] và [tex](H_2)[/tex] bằng nhau thì [tex]V_{H_1}=V_{H_2}[/tex]
+ nếu khối đa diện (H) được chia thành 2 phần [tex](H_1)[/tex] và [tex](H_2)[/tex] thì [tex]V_{(H)}=V_{(H_1)}+V_{(H_2)}[/tex]
- công thức tính thể tích của khối đa diện thường gặp:
+ hình lăng trụ:
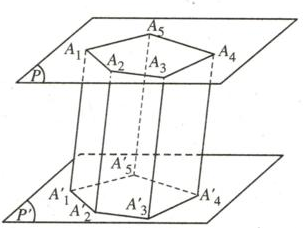
[tex]V=S.h[/tex]
với: S là diện tích 1 mặt đáy, h là chiều cao của hình lăng trụ.
ví dụ: cho hình lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh a, cạnh bên bằng a. hình chiếu vuông góc của A' xuống mặt đáy trùng với trọng tâm G của tam giác ABC. tính thể tích khối lăng trụ.
diện tích 1 mặt đáy ABC: [tex]S_{ABC}=a.a.\frac{\sqrt{3}}{4}=a^2.\frac{\sqrt{3}}{4}[/tex]
ta có A'G chính là đường cao hạ từ đỉnh A' của hình lăng trụ.
ta tính được [tex]AG=a.\frac{\sqrt{3}}{3}[/tex]
áp dụng pytago cho tam giác AGA', ta tính được [tex]A'G=a.\frac{\sqrt{6}}{3}[/tex]
từ đó, thể tích của hình lăng trụ là:
[tex]V=S_{ABC}.A'G=a^2.\frac{\sqrt{3}}{4}.a.\frac{\sqrt{6}}{3}=a^3.\frac{\sqrt{2}}{4}[/tex]
+ hình chóp:
[tex]V=\frac{1}{3}S.h[/tex]
với: S là diện tích mặt đáy, h là chiều cao của khối chóp.
ví dụ: Tính thể tích của hình chóp S.ABC có tam giác ABC là tam giác vuông tại B, có [tex]AB=a\sqrt{2}[/tex], [tex]AC=a\sqrt{3}[/tex], SA vuông góc với mặt phẳng đáy, [tex]SB=a\sqrt{3}[/tex].
xét tam giác ABC vuông tại B, theo pytago ta tính được [tex]BC=a[/tex]
diện tích tam giác ABC: [tex]S=\frac{1}{2}AB.BC=\frac{1}{2}.a\sqrt{2}.a=a^2.\frac{\sqrt{2}}{2}[/tex]
SA là đường cao của hình chóp hạ từ đỉnh A.
xét tam giác SAB vuông tại A, ta tính được [tex]SA=a[/tex].
thể tích khối chóp [tex]S.ABC[/tex]là [tex]V=\frac{1}{3}S.SA=\frac{1}{3}.a^2.\frac{\sqrt{2}}{2}.a=a^3.\frac{\sqrt{2}}{6}[/tex]
2. Kiến thức bổ sung
- tỉ số thể tích: cho hình chóp S.ABC, trên tia SA, SB, SC lấy các điểm A', B', C'. khi đó ta có:
[tex]\frac{V_{S.A'B'C'}}{V_{S.ABC}}=\frac{SA'}{SA}.\frac{SB'}{SB}.\frac{SC'}{SC}[/tex]
- nếu H' là ảnh của H qua phép dời hình thì [tex]V_{H'}=V_{H}[/tex]
- nếu H' là ảnh của H qua phép vị tự tỉ số k thì [tex]V_{H'}=|k|^3.V_{H}[/tex]
- thể tích khối đa diện là thể tích phần không gian mà hình đa diện chiếm, kể cả hình đa diện đó.
- nếu gọi khối đa diện là (H), người ta chứng minh được rằng: thể tích của khối đa diện luôn dương, tức là [tex]V_{(H)}>0[/tex]
- tính chất của thể tích khối đa diện:
+ nếu (H) là khối lập phương có cạnh bằng 1 thì [tex]V_{(H)}=1[/tex]
+ nếu 2 khối đa diện [tex](H_1)[/tex] và [tex](H_2)[/tex] bằng nhau thì [tex]V_{H_1}=V_{H_2}[/tex]
+ nếu khối đa diện (H) được chia thành 2 phần [tex](H_1)[/tex] và [tex](H_2)[/tex] thì [tex]V_{(H)}=V_{(H_1)}+V_{(H_2)}[/tex]
- công thức tính thể tích của khối đa diện thường gặp:
+ hình lăng trụ:
[tex]V=S.h[/tex]
với: S là diện tích 1 mặt đáy, h là chiều cao của hình lăng trụ.
ví dụ: cho hình lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh a, cạnh bên bằng a. hình chiếu vuông góc của A' xuống mặt đáy trùng với trọng tâm G của tam giác ABC. tính thể tích khối lăng trụ.
diện tích 1 mặt đáy ABC: [tex]S_{ABC}=a.a.\frac{\sqrt{3}}{4}=a^2.\frac{\sqrt{3}}{4}[/tex]
ta có A'G chính là đường cao hạ từ đỉnh A' của hình lăng trụ.
ta tính được [tex]AG=a.\frac{\sqrt{3}}{3}[/tex]
áp dụng pytago cho tam giác AGA', ta tính được [tex]A'G=a.\frac{\sqrt{6}}{3}[/tex]
từ đó, thể tích của hình lăng trụ là:
[tex]V=S_{ABC}.A'G=a^2.\frac{\sqrt{3}}{4}.a.\frac{\sqrt{6}}{3}=a^3.\frac{\sqrt{2}}{4}[/tex]
+ hình chóp:
[tex]V=\frac{1}{3}S.h[/tex]
với: S là diện tích mặt đáy, h là chiều cao của khối chóp.
ví dụ: Tính thể tích của hình chóp S.ABC có tam giác ABC là tam giác vuông tại B, có [tex]AB=a\sqrt{2}[/tex], [tex]AC=a\sqrt{3}[/tex], SA vuông góc với mặt phẳng đáy, [tex]SB=a\sqrt{3}[/tex].
xét tam giác ABC vuông tại B, theo pytago ta tính được [tex]BC=a[/tex]
diện tích tam giác ABC: [tex]S=\frac{1}{2}AB.BC=\frac{1}{2}.a\sqrt{2}.a=a^2.\frac{\sqrt{2}}{2}[/tex]
SA là đường cao của hình chóp hạ từ đỉnh A.
xét tam giác SAB vuông tại A, ta tính được [tex]SA=a[/tex].
thể tích khối chóp [tex]S.ABC[/tex]là [tex]V=\frac{1}{3}S.SA=\frac{1}{3}.a^2.\frac{\sqrt{2}}{2}.a=a^3.\frac{\sqrt{2}}{6}[/tex]
2. Kiến thức bổ sung
- tỉ số thể tích: cho hình chóp S.ABC, trên tia SA, SB, SC lấy các điểm A', B', C'. khi đó ta có:
[tex]\frac{V_{S.A'B'C'}}{V_{S.ABC}}=\frac{SA'}{SA}.\frac{SB'}{SB}.\frac{SC'}{SC}[/tex]
- nếu H' là ảnh của H qua phép dời hình thì [tex]V_{H'}=V_{H}[/tex]
- nếu H' là ảnh của H qua phép vị tự tỉ số k thì [tex]V_{H'}=|k|^3.V_{H}[/tex]