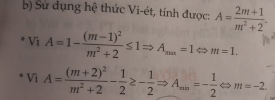View attachment 209447
Cho em hỏi với những bài như này thì hướng tư duy tách ghép như thế nào để có thể tìm được A min và A max ạ .Em cảm ơn ạ
thuhuyenefLớp 9 thì có cách khác rồi em nhé. Đưa về phương trình bậc 2 ẩn m, rồi giải điều kiện để phương trình có nghiệm như sau:
[imath]A(m^2+2) = 2m+1[/imath]
[imath]\Rightarrow Am^2 -2m +(2A-1) = 0[/imath] (1)
TH1 : Nếu [imath]A= 0 \Rightarrow m=\dfrac{-1}{2}[/imath]
TH2: Nếu [imath]A\ne 0[/imath], thì (1) là phương trình bậc 2 có
[imath]\Delta' = 1^2 - A.(2A-1) = (1-A)(2A-1) \geq 0[/imath]
Từ đó bạn giải min max của A, dấu = xảy ra khi [imath]m = \dfrac{-b'}{a} = \dfrac{1}{A}[/imath]
Ngoài ra mời bạn tham khảo Phương trình bậc hai một ẩn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
