leduymanh2005
[imath]1/[/imath]
Chọn trục [imath]Ou[/imath] thẳng đứng hướng lên
[imath]a/[/imath]
Xét dao động điểm [imath]O[/imath]:
Ban đầu [imath]O[/imath] ở vị trí cân bằng và đang đi lên theo chiều dương, sau thời gian [imath]\Delta t[/imath] đi xuống điểm thấp nhất là biên âm
Góc quét là: [imath]\Delta \varphi = \dfrac{3\pi}{2} \ rad[/imath]
Thời gian [imath]\Delta t[/imath] là: [imath]\Delta t = \dfrac{\Delta \varphi}{\omega}=\dfrac{\dfrac{3\pi}{2}}{\dfrac{2\pi}{T}}=\dfrac{3T}{4}[/imath] | 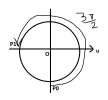 |
[imath]b/[/imath] Điểm [imath]M[/imath] đang dao động đi lên.
[imath]2/[/imath]
[imath]a/[/imath]
[imath]A,B[/imath] cùng pha với nguồn [imath]O[/imath] nên hai điểm đều thuộc các đường tròn tâm [imath]O[/imath] như hình vẽ, trong đó [imath]A[/imath] nằm đường thứ [imath]6[/imath], [imath]B[/imath] nằm đường thứ [imath]7[/imath] vì trên [imath]OA,OB[/imath] lần lượt có [imath]6,7[/imath] điểm cùng pha với [imath]O[/imath].
Để trên [imath]AB[/imath] có [imath]6[/imath] điểm cùng pha [imath]O[/imath] thì [imath]AB[/imath] tiếp tuyến với đường tròn thứ [imath]4[/imath] như hình vẽ, gọi [imath]H[/imath] là tiếp điểm.
[imath]OA=6\lambda = 54cm[/imath]
[imath]OB=7\lambda = 63cm[/imath]
[imath]OH=4\lambda = 24cm[/imath]
Áp dụng Pytago trong hai tam giác [imath]AHO[/imath] và [imath]BHO[/imath] vuông tại [imath]H[/imath] dễ dàng tìm được [imath]AH = 6\sqrt{65}cm[/imath] và [imath]BH = 3\sqrt{377}cm[/imath]
Vậy [imath]AB=AH+BH \approx 106,62cm[/imath] | 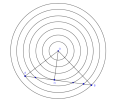 |
[imath]b/[/imath]
Độ lệch pha giữa [imath]A[/imath] và [imath]C[/imath]: [imath]\Delta \varphi _{AC}=\dfrac{2\pi . 16,5}{9}=\dfrac{11\pi}{3} = 3\pi + \dfrac{2\pi}{3} \ rad[/imath]
[imath]C[/imath] trên đoạn [imath]OA[/imath] tức là [imath]C[/imath] nằm giữa [imath]O[/imath] và [imath]A[/imath], suy ra [imath]C[/imath] nhanh pha hơn [imath]A[/imath].
- Khi [imath]A[/imath] đến điểm thấp nhất (biên âm) thì điểm pha của nó là [imath]P_A[/imath] trên hình. [imath]A[/imath] chậm pha hơn [imath]C[/imath] nên từ điểm pha [imath]P_A[/imath], quay cùng chiều dương cung [imath]\Delta \varphi _{AC}[/imath] ta xác định được điểm pha của [imath]C[/imath] là [imath]P_C[/imath] trên hình.
[imath]C[/imath] đi từ vị trí này đến vị trí cao nhất (biên dương) thì góc quét là [imath]\dfrac{4\pi}{3}[/imath]
Thời gian [imath]C[/imath] đến vị trí cao nhất kể từ khi [imath]A[/imath] đến vị trí thấp nhất:
[imath]t=\dfrac{\dfrac{4\pi}{3}}{\omega}=\dfrac{\dfrac{4\pi}{3}}{\dfrac{2\pi}{T}}=\dfrac{1}{3}s[/imath]
- Phương trình dao động của phần tử sóng:
+ tại [imath]O[/imath]: [imath]u_O=5\cos (\omega t - \dfrac{\pi}{2}) = 5\angle \dfrac{\pi}{2}[/imath]
+ tại [imath]A[/imath]: [imath]u_A=5\cos (\omega t - \dfrac{\pi}{2}-\dfrac{2\pi .OA}{\lambda})=5\angle -\dfrac{25}{2}\pi[/imath]
+ tại [imath]C[/imath]: [imath]u_C = 5\cos (\omega t - \dfrac{\pi}{2}- \dfrac{2\pi . (OA-16,5)}{\lambda})=5\angle-\dfrac{53}{6}\pi[/imath]
[imath]\Rightarrow u_A-u_C = 5\angle-\dfrac{\pi}{6}=5\cos(\omega t - \dfrac{\pi}{6})[/imath]
[imath]\Rightarrow (u_A-u_C)_{max}=5cm[/imath]
Khoảng cách cực đại giữa hai điểm [imath]A,C[/imath] là:
[imath]d=\sqrt{16,5^2+(u_A-u_C)_{max}^2}=17,24cm[/imath] | 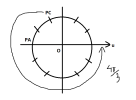 |
Chúc bạn học tốt!
-----
Xem thêm:
[Giao thoa sóng] - Cực đại, cực tiểu và phương trình giao thoa
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.