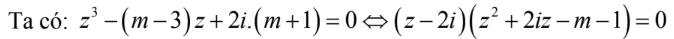Hỏi có tất cả bao nhiêu giá trị nguyên của tham số [imath]m \in [-40; 40][/imath] để phương trình phức [imath]z^3 -(m-3)z+2i(m+1)=0[/imath]
có đúng 3 nghiệm phức thuần ảo?
A.40 .
B.41 .
C.39 .
D.78 .
Để giải bài này ta lm như sau :
View attachment 212233
Nhưng ngay chỗ này e không hiểu ạ ? ai giúp e với !
superchemistỞ đó là bước phân tích thành nhân tử nhé bạn.
Thông thường thì những bài tập này phương trình nếu có bậc [imath]3[/imath] thì sẽ có thể phân tích được thành nhân tử để đưa về phương trình bậc [imath]2[/imath].
Ta biết rằng nếu đa thức [imath]x^n+a_{n-1}x^{n-1}+...+a_1x+a_0=0[/imath] có nghiệm [imath]x_0[/imath] thì [imath]a_0[/imath] chia hết cho [imath]x_0[/imath]. Ở đây cũng vậy.
Ta có [imath]2i(m+1)[/imath] sẽ chia hết cho nghiệm của phương trình trên, nên ta sẽ
nhẩm nghiệm đẹp có thể là [imath]\pm 1, \pm 2, \pm i, \pm m+1, \pm 2i, \pm 2(m+1), \pm 2i(m+1)[/imath].
Mà đề bài yêu cầu là nghiệm phức thuần ảo nên ta sẽ chú ý đến [imath]\pm i[/imath] và [imath]\pm 2i[/imath] thôi. Thử chọn thì ta thấy [imath]2i[/imath] là nghiệm.
Khi đó ta phân tích được [imath](z-2i)(...)[/imath]. Và khi đó ta đã đưa về phương trình bậc 2.
Nếu còn thắc mắc chỗ nào bạn hãy trả lời dưới topic này để được hỗ trợ nhé. Chúc bạn học tốt ^^
Ngoài ra, bạn tham khảo kiến thức tại topic này nha
Chinh phục kì thi THPTQG môn Toán 2022
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
