- 27 Tháng mười 2018
- 3,742
- 3,706
- 561
- Hà Nội
- Trường Đại học Bách Khoa Hà Nội
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Số phức là chương cuối cùng của phần đại số và giải tích 12. Cũng chiếm khoảng 5-6 câu trong đề thi đại học. Trong đó có 1 câu vận dụng cao, về tìm cực trị số phức. Còn lại 4-5 câu ở mức dễ đến khá.
Và sau đây là 1 số kiến thức cơ bản cần nhớ của chương: số phức sinh ra nhằm đáp ứng mong muốn mọi phương trình đều có nghiệm. Như các bạn đã biết thì phương trình kiểu [tex]x^2+1=0[/tex] là vô nghiệm trên tập số thực. Khi mở rộng lên tập số phức thì nó lại có nghiệm.
Số phức có dạng :
[tex]z=a+b.i[/tex](a,b thuộc R) và [tex]i^2=-1[/tex]
a: gọi là phần thực của số phức.
b: là phần ảo số phức ( lưu ý chỉ là hệ số b chứ không phải cả b.i)
Nếu b=0 => Ta có số thực. Còn nếu a=0 thì ta có 1 số thuần ảo.
Module của số phức.
Để hiểu về module của số phức thì trước hết đi đến khái niệm biểu diễn hình học số phức. Mỗi số phức được biểu diễn bởi 1 điểm tương ứng duy nhất trong mp tọa độ Oxy. Với số phức [tex]z=a+b.i[/tex] thì điểm biểu diễn của nó là M(a;b).
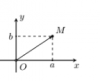
Như vậy có thể thấy trục Ox chính là trục số thực mà ta đã học.
Module của số phức z, khí hiệu |z| chính là độ dài đoạn thẳng OM. Vậy : [tex]|z|=\sqrt{a^2+b^2}[/tex]
Số phức liên hợp: kí hiệu [tex]\overline{z}=a-bi[/tex]
Như vậy ta có tính chất sau: [tex]z.\overline{z}=(a-bi)(a+bi)=a^2+b^2=z^2[/tex]
Thêm 1 số tính chất liên quan đến module số phức: với 2 số phức z và z' :
[tex]|z.z'|=|z|.|z'|[/tex]
[tex]|\frac{z}{z'}|=\frac{|z|}{|z'|}[/tex]
[tex]||z|-|z'||\leq |z+(-)z'|\leq |z|+|z'|[/tex]
Các phép toán thực hiện đối với số phức : +,-,x,/ cũng tương tự như phép +, -, x, / đối với đa thức, chỉ cần lưu ý [tex]i^2=-1[/tex] để có thể tối giản biểu thức thu được:
[tex](a+bi)+(c+di)=(a+c)+i(b+d)[/tex]
[tex](a+bi)-(c+di)=(a-c)+i(b-d)[/tex]
[tex](a+bi).(c+di)=ac+i(bc+ad)+bd.i^2=ac+i(bc+ad)-bd[/tex]
[tex]\frac{a+bi}{c+di}=\frac{(a+bi)(c-di)}{(c+di)(c-di)}=\frac{ac+bd-(ad-bc)i}{c^2+d^2}[/tex]
Lũy thừa của đơn vị ảo : chia làm 4 trường hợp:
Với n thuộc Z thì ta có:
[tex]i^n=1[/tex] khi n chia hết cho 4
[tex]i^n=i[/tex] khi n chia 4 dư 1
[tex]i^n=-1[/tex] khi n chia 4 dư 2
[tex]i^n=-i[/tex] khi n chia 4 dư 3
Giải phương trình bậc 2 với hệ số thực:
Xét phương trình bậc 2 : [tex]ax^2+bx+c(a\neq 0)[/tex]
Có [tex]\Delta =b^2-4ac[/tex] , khi [TEX]\Delta\geq0[/TEX] thì công thức nghiệm như đã biết:
[tex]x_1=\frac{-b-\sqrt{\Delta }}{2a};x_2=\frac{-b+\sqrt{\Delta }}{2a}[/tex]
Còn khi [TEX]\Delta\leq0[/TEX] thì phương trình có nghiệm phức:
[tex]x_1=\frac{-b-i\sqrt{|\Delta| }}{2a};x_2=\frac{-b+i\sqrt{|\Delta| }}{2a}[/tex]
Đó là các kiến thức cơ bản về toàn chương số phức lớp 12. Các bạn chỉ cần nắm được là đã đi chiến đấu đề thi được rồi
Và sau đây là 1 số kiến thức cơ bản cần nhớ của chương: số phức sinh ra nhằm đáp ứng mong muốn mọi phương trình đều có nghiệm. Như các bạn đã biết thì phương trình kiểu [tex]x^2+1=0[/tex] là vô nghiệm trên tập số thực. Khi mở rộng lên tập số phức thì nó lại có nghiệm.
Số phức có dạng :
[tex]z=a+b.i[/tex](a,b thuộc R) và [tex]i^2=-1[/tex]
a: gọi là phần thực của số phức.
b: là phần ảo số phức ( lưu ý chỉ là hệ số b chứ không phải cả b.i)
Nếu b=0 => Ta có số thực. Còn nếu a=0 thì ta có 1 số thuần ảo.
Module của số phức.
Để hiểu về module của số phức thì trước hết đi đến khái niệm biểu diễn hình học số phức. Mỗi số phức được biểu diễn bởi 1 điểm tương ứng duy nhất trong mp tọa độ Oxy. Với số phức [tex]z=a+b.i[/tex] thì điểm biểu diễn của nó là M(a;b).
Như vậy có thể thấy trục Ox chính là trục số thực mà ta đã học.
Module của số phức z, khí hiệu |z| chính là độ dài đoạn thẳng OM. Vậy : [tex]|z|=\sqrt{a^2+b^2}[/tex]
Số phức liên hợp: kí hiệu [tex]\overline{z}=a-bi[/tex]
Như vậy ta có tính chất sau: [tex]z.\overline{z}=(a-bi)(a+bi)=a^2+b^2=z^2[/tex]
Thêm 1 số tính chất liên quan đến module số phức: với 2 số phức z và z' :
[tex]|z.z'|=|z|.|z'|[/tex]
[tex]|\frac{z}{z'}|=\frac{|z|}{|z'|}[/tex]
[tex]||z|-|z'||\leq |z+(-)z'|\leq |z|+|z'|[/tex]
Các phép toán thực hiện đối với số phức : +,-,x,/ cũng tương tự như phép +, -, x, / đối với đa thức, chỉ cần lưu ý [tex]i^2=-1[/tex] để có thể tối giản biểu thức thu được:
[tex](a+bi)+(c+di)=(a+c)+i(b+d)[/tex]
[tex](a+bi)-(c+di)=(a-c)+i(b-d)[/tex]
[tex](a+bi).(c+di)=ac+i(bc+ad)+bd.i^2=ac+i(bc+ad)-bd[/tex]
[tex]\frac{a+bi}{c+di}=\frac{(a+bi)(c-di)}{(c+di)(c-di)}=\frac{ac+bd-(ad-bc)i}{c^2+d^2}[/tex]
Lũy thừa của đơn vị ảo : chia làm 4 trường hợp:
Với n thuộc Z thì ta có:
[tex]i^n=1[/tex] khi n chia hết cho 4
[tex]i^n=i[/tex] khi n chia 4 dư 1
[tex]i^n=-1[/tex] khi n chia 4 dư 2
[tex]i^n=-i[/tex] khi n chia 4 dư 3
Giải phương trình bậc 2 với hệ số thực:
Xét phương trình bậc 2 : [tex]ax^2+bx+c(a\neq 0)[/tex]
Có [tex]\Delta =b^2-4ac[/tex] , khi [TEX]\Delta\geq0[/TEX] thì công thức nghiệm như đã biết:
[tex]x_1=\frac{-b-\sqrt{\Delta }}{2a};x_2=\frac{-b+\sqrt{\Delta }}{2a}[/tex]
Còn khi [TEX]\Delta\leq0[/TEX] thì phương trình có nghiệm phức:
[tex]x_1=\frac{-b-i\sqrt{|\Delta| }}{2a};x_2=\frac{-b+i\sqrt{|\Delta| }}{2a}[/tex]
Đó là các kiến thức cơ bản về toàn chương số phức lớp 12. Các bạn chỉ cần nắm được là đã đi chiến đấu đề thi được rồi
