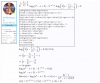
$9^{\left |x-\dfrac{1}{2} \right |+\dfrac{1}{8}}.\log_2(x^2-x+2)-3^{-x^2+x}.\log_2 \left ( 2 \left | x-\dfrac{1}{2} \right |+\dfrac{7}{4} \right ) = 0$
$\Leftrightarrow \left [ \begin{matrix}
9^{\left |x-\dfrac{1}{2} \right |+\dfrac{1}{8}} = 0 \ (1) \\
\log_2(x^2-x+2)-3^{-x^2+x} = 0 \ (2) \\
\log_2 \left ( 2 \left | x-\dfrac{1}{2} \right |+\dfrac{7}{4} \right ) = 0 \ (3)
\end{matrix}\right. \\
9^{\left |x-\dfrac{1}{2} \right |+\dfrac{1}{8}} = 0 \ (1) \\
\Leftrightarrow \left |x-\dfrac{1}{2} \right |+\dfrac{1}{8} = 1 \\
\Leftrightarrow \left |x-\dfrac{1}{2} \right | = \dfrac{7}{8} \\
\Leftrightarrow \left [ \begin{matrix}
x - \dfrac{1}{2} = \dfrac{7}{8} \\
x - \dfrac{1}{2} = - \dfrac{7}{8}
\end{matrix}\right. \\
\Leftrightarrow \left [ \begin{matrix}
x = \dfrac{11}{8} \\
x = - \dfrac{3}{8}
\end{matrix}\right.$
$\log_2 \left ( 2 \left | x-\dfrac{1}{2} \right |+\dfrac{7}{4} \right ) = 0 \ (2) \\
\Leftrightarrow 2 \left | x-\dfrac{1}{2} \right |+\dfrac{7}{4} = 1$
$\Leftrightarrow \left | x-\dfrac{1}{2} \right |= - \dfrac{3}{8}$ (Vô lý)
=> Vô nghiệm
$\log_2(x^2-x+2)-3^{-x^2+x} = 0 \ (3) \\
\log_2(x^2-x+2) = 3^{-x^2+x}$
Đặt $u(x) = \log_2(x^2-x+2) \Rightarrow u'(x)=\dfrac{2x-1}{(x^2-x+2) \ln{2}}$
$v(x)=3^{-x^2+x} \Rightarrow v'(x) = 3^{-x^2+x}.(-2x+1)$
*bí lù :v dự đoán là vô nghiệm :v *
(chắc xài tính đơn điệu của hàm quá :v)
Kết luận: pt đầu có 02 nghiệm thực phân biệt
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.