[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Bài 3: Bất phương trình bậc nhất 2 ẩn
I) Bất phương trình bậc nhất 2 ẩn- Bất phương trình bậc nhất 2 ẩn [imath]x;y[/imath] có dạng tổng quát là
[imath]ax + by \le c (ax + by \ge c; ax + by < c; ax + by > c)[/imath]
trong đó [imath]a;b;c[/imath] là những số thực đã cho, [imath]a[/imath] và [imath]b[/imath] không đồng thời bằng [imath]0[/imath], [imath]x[/imath] và [imath]y[/imath] là các ẩn số- Cặp số [imath](x_o;y_o)[/imath] được gọi là 1 nghiệm của BPT bậc nhất 2 ẩn [imath]ã + by \le c[/imath] nếu BĐT [imath]ax_o + by_o \le c[/imath] đúng
VD1: BPT nào sau đây là BPT bậc nhất 2 ẩn:
a) [imath]2x + 3y < 1[/imath]
b) [imath]2x^2 + 3y > 1[/imath]
Lời giải: a) Là BPT bậc nhất 2 ẩn ; b) Không là BPT bậc nhất 2 ẩn vì có [imath]x^2[/imath]
VD2: Cho BPT [imath]2x + y \le 1[/imath]. Cặp số nào sau đây là nghiệm của BPT:
a) [imath](0;0)[/imath]
b) [imath](2;0)[/imath]
Lời giải:
a) Ta có: [imath]2.0 + 0 < 1[/imath] nên [imath](0;0)[/imath] là cặp nghiệm của BPT
b) Ta có: [imath]2.2 + 0 > 1[/imath] nên [imath](2;0)[/imath] không là cặp nghiệm của BPT
II) Biểu diễn miền nghiệm của BPT bậc nhất 2 ẩn trên mặt phẳng tọa độ
- Trong mp tọa độ [imath]Oxy[/imath], tập hợp các điểm có tọa độ là nghiệm của BPT [imath]ax + by \le 0[/imath] được gọi là miền nghiệm của BPT đó
- Người ta chứng minh được rằng đường thẳng [imath]d[/imath] có phương trình [imath]ax + by = c[/imath] chia mặt phẳng tọa độ [imath]Oxy[/imath] thành 2 nửa mặt phẳng bờ [imath]d[/imath]:
- Một nửa mặt phẳng ( không kể bờ [imath]d[/imath]) gồm các điểm có tọa độ [imath](x;y)[/imath] thỏa mãn [imath]ax + by < 0[/imath]
- Bờ [imath]d[/imath] gồm các điểm có tọa độ [imath](x;y)[/imath] thỏa mãn [imath]ax +by = c[/imath]
Cách biểu diễn miền nghiệm của BPT bậc nhất 2 ẩn [imath]ax + by \ge c[/imath]
- Vẽ đường thẳng [imath]d : ax + by = c[/imath] trên mặt phẳng [imath]Oxy[/imath]
- Lấy một điểm [imath]M(x_o;y_o)[/imath] không thuộc [imath]d[/imath]
- Tính [imath]ax_o + by_o[/imath] và so sánh với [imath]c[/imath]
- Nếu [imath]ax_o + by_o < c[/imath] thì nửa mặt phẳng [imath]d[/imath] chứa [imath]M[/imath] là miền nghiệm của BPT và ngược lại
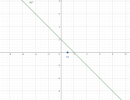
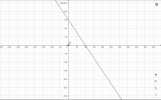
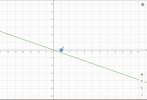
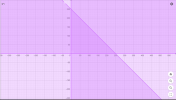
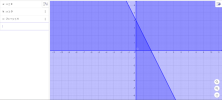
B1: Vẽ đường thẳng [imath]x + y = 2[/imath]
B2: Chọn điểm [imath]M(1;0)[/imath]. Ta có: [imath]1 + 0 < 2[/imath]
Vậy miền nghiệm của BPT [imath]x + y < 2[/imath] là nửa mp bờ [imath]d[/imath] chứa [imath]M[/imath]