Toán 10 [SGK Mới] Bài 8: Tổng và hiệu của hai vectơ

[Alice_www]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

BÀI 8: TỔNG VÀ HIỆU CỦA HAI VECTƠ​

1. Tổng của hai vectơ


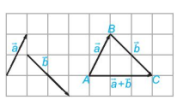
Cho hai vectơ [imath]\overrightarrow{a},\overrightarrow{b}.[/imath] Lấy một điểm A tùy ý và vẽ [imath]\overrightarrow{AB}=\overrightarrow{a}, \overrightarrow{BC}=\overrightarrow{b}[/imath]. Khi đó vectơ [imath]\overrightarrow{AC}[/imath] được gọi là tổng của hai vectơ [imath]\overrightarrow{a}[/imath] và [imath]\overrightarrow{b}[/imath] và được kí hiệu là [imath]\overrightarrow{a}+\overrightarrow{b}[/imath]

Phép lấy tổng của hai vectơ được gọi là phép cộng vectơ.

Cho hình bình hành ABCD. Tìm mối quan hệ giữa hai vectơ [imath]\overrightarrow{AB}+\overrightarrow{AD}[/imath] và [imath]\overrightarrow{AC}[/imath]

[imath]\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}[/imath]

Chú ý: Hai quy tắc dưới này thường xuyên được dùng trong các bài toán cần dùng vectơ

Quy tắc ba điểm: Với ba điểm bất kì A,B,C, ta có $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$

Quy tắc hình bình hành: Nếu ABCD là một hình bình hành thì $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$

Tính chất phép cộng hai vectơ
Với ba vectơ [imath]\overrightarrow{a}, \overrightarrow{b},\overrightarrow{c}[/imath] tùy ý:
+ Tính giao hoán: [imath]\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{b}+\overrightarrow{a}[/imath]
+ Tính kết hợp [imath](\overrightarrow{a}+\overrightarrow{b})+\overrightarrow{c}=\overrightarrow{a}+(\overrightarrow{b}+\overrightarrow{c})[/imath]
+ Tính chất của vectơ-không: [imath]\overrightarrow{a}+\overrightarrow{0}=\overrightarrow{0}+\overrightarrow{a}=\overrightarrow{a}[/imath]

Luyện tập 1: Cho hình thoi ABCD với cạnh có độ dài bằng 1 và [imath]\widehat{BAD}=120^\circ[/imath]. Tính độ dài của các vectơ [imath]\overrightarrow{CB}+\overrightarrow{CD}, \overrightarrow{DB}+\overrightarrow{CD}+ \overrightarrow{BA}[/imath]

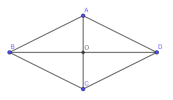
+) [imath]\widehat{BAD}=120^\circ\Rightarrow \widehat{BAC}=60^\circ[/imath]
[imath]\Rightarrow \Delta ABC[/imath] đều[imath]\Rightarrow AC=1[/imath]
[imath]\overrightarrow{CB}+\overrightarrow{CD}=\overrightarrow{CB}+\overrightarrow{BA}=\overrightarrow{CA}[/imath]
[imath]\Rightarrow |\overrightarrow{CB}+\overrightarrow{CD}|=|\overrightarrow{CA}|=CA=1[/imath]

+) Gọi O là giao điểm của AC và BD
[imath]\overrightarrow{DB}+\overrightarrow{CD}+ \overrightarrow{BA}=2 \overrightarrow{DO}+2 \overrightarrow{CD}=2 \overrightarrow{CO}[/imath]
[imath]\Rightarrow |\overrightarrow{DB}+\overrightarrow{CD}+ \overrightarrow{BA}|=2CO=AC=1[/imath]

2. Hiệu của hai vectơ

- Vectơ có cùng độ dài và ngược hướng với [imath]\overrightarrow{a}[/imath] được gọi là vectơ đối của vectơ [imath]\overrightarrow{a}[/imath], được kí hiệu là [imath]-\overrightarrow{a}[/imath].

- Vectơ [imath]\overrightarrow{a}+(-\overrightarrow{b}[/imath] được gọi là hiệu của hai vectơ [imath]\overrightarrow{a}[/imath] và [imath]\overrightarrow{b}[/imath], được kí hiệu là [imath]\overrightarrow{a}-\overrightarrow{b}[/imath].

- Phép lấy hiệu hai vectơ được gọi là phép trừ vectơ.

Quy tắc hiệu: Với ba điểm O,M,N, ta có $\overrightarrow{MN}=\overrightarrow{ON}-\overrightarrow{OM}$

Luyện tập 2. Cho tứ giác ABCD. Gọi M,N lần lượt là trung điểm của các cạnh AB,CD và O là trung điểm của MN. Chứng minh rằng [imath]\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{0}[/imath]

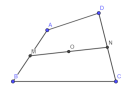
M,N,O lần lượt là trung điểm của AB,CD,MN nên
[imath]\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{0};\overrightarrow{NC}+\overrightarrow{ND}=\overrightarrow{0}; \overrightarrow{OM}+\overrightarrow{ON}=\overrightarrow{0}[/imath]

[imath]\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{OM}+\overrightarrow{MA}+\overrightarrow{OM}+\overrightarrow{MB}+\overrightarrow{ON}+\overrightarrow{ND}+\overrightarrow{ON}+\overrightarrow{NC}[/imath]

[imath]=2(\overrightarrow{OM}+\overrightarrow{ON})+(\overrightarrow{MA}+\overrightarrow{MB})+(\overrightarrow{ND}+\overrightarrow{NC})=\overrightarrow{0}[/imath]

Chúc các bạn học tốt nha
Xem thêm: Trọn bộ kiến thức học tốt các môn

 

[Alice_www]

BÀI TẬP​

4.6 Cho bốn điểm A,B,C,D. Chứng minh rằng:

a) [imath]\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DA}=\overrightarrow{0}[/imath]

[imath]VT=(\overrightarrow{AB}+\overrightarrow{BC})+(\overrightarrow{CD}+\overrightarrow{DA})=\overrightarrow{AC}+\overrightarrow{CA}=\overrightarrow{0}[/imath]

b) [imath]\overrightarrow{AC}-\overrightarrow{AD}=\overrightarrow{BC}-\overrightarrow{BD}[/imath]

[imath]\Leftrightarrow \overrightarrow{DC}=\overrightarrow{DC}[/imath] (luôn đúng)

4.7 Cho hình bình hành ABCD. Hãy tìm điểm M để [imath]\overrightarrow{BM}=\overrightarrow{AB}+\overrightarrow{AD}[/imath]. Tìm mối quan hệ giữa hai vectơ [imath]\overrightarrow{CD}[/imath] và [imath]\overrightarrow{CM}[/imath]

[imath]\overrightarrow{BM}=\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}[/imath]

[imath]\Rightarrow BMCA[/imath] là hình bình hành [imath]\Rightarrow \overrightarrow{CM}=\overrightarrow{AB}[/imath]

[imath]ABCD[/imath] là hình bình hành [imath]\Rightarrow \overrightarrow{AB}=\overrightarrow{DC}[/imath]

Suy ra [imath]\overrightarrow{CM}=-\overrightarrow{CD}[/imath]

4.8 Cho tam giác đều ABC có cạnh bằng a. Tính độ dài của các vectơ [imath]\overrightarrow{AB}-\overrightarrow{AC}, \overrightarrow{AB}+\overrightarrow{AC}[/imath]

[imath]|\overrightarrow{AB}-\overrightarrow{AC}|=|\overrightarrow{CB}|=CB=a[/imath]

Kẻ hình bình hành ABDC. Gọi H là trung điểm của BC

[imath]\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BD}=\overrightarrow{AD}=2\overrightarrow{AH}[/imath]

[imath]\Rightarrow |\overrightarrow{AB}+\overrightarrow{AC}|=2AH=2\sqrt{AB^2-\dfrac{BC^2}4}=\sqrt3[/imath]


4.9 Cho biểu diễn lực [imath]\overrightarrow{F_1}, \overrightarrow{F_2}[/imath] cùng tác động lên một vật, cho [imath]|\overrightarrow{F_1}|=3 N, |\overrightarrow{F_2}=2 N[/imath]. Tính độ lớn của hợp lực [imath]\overrightarrow{F_1}+\overrightarrow{F_2}[/imath].

[imath]\overrightarrow{F_1}+\overrightarrow{F_2}=\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AD}\Rightarrow |\overrightarrow{F_1}+\overrightarrow{F_2}|=AD[/imath]

[imath]\widehat{ABD}=180^\circ-\widehat{CAB}=60^\circ[/imath]

[imath]AD=\sqrt{AB^2+BD^2-2AB.DB.\cos 60^\circ}=\sqrt7 (N)[/imath]



4.10

Ta có [imath]\overrightarrow{AB}, \overrightarrow{A'B'}[/imath] là vận tốc dòng nước
[imath]AE,A'F[/imath] là con đường mà thuyền đi, 2 đường thẳng tạo với bờ 1 góc như nhau

Từ B kẻ vuông góc cắt AE tại C. Dựng hình bình hành ABCD.

Trên A'F lấy điểm C' sao cho [imath]\overrightarrow{B'C'}=\overrightarrow{AD}[/imath]. Dựng hình bình hành A'B'C'D'.

[imath]\Rightarrow \overrightarrow{AD},\overrightarrow{A'D'}[/imath] là vận tốc riêng của con tàu
[imath]\overrightarrow{AC},\overrightarrow{A'C'}[/imath] là vận tốc thực của tàu.

[imath]A'C'^2=A'B'^2+A'D'^2-2A'B'A'D'\cos \widehat{C'D'A'}[/imath]
[imath]<AB^2+AD^2=AC^2 (\cos \widehat{C'D'A'}>0)[/imath]
[imath]\Rightarrow A'C'<AC[/imath]
Vậy tàu đi về hạ lưu sẽ sang bờ trước