[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
VECTƠ TRONG MẶT PHẲNG TỌA ĐỘ
1. Tọa độ của vectơ
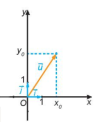
Trên mặt phẳng xét hai trục Ox, Oy có chung gốc O và vuông góc với nhau.
Vectơ đơn vị của trục Ox là [imath]\overrightarrow{i}=(1,0)[/imath], vectơ đơn vị của trục Oy là [imath]\overrightarrow{j}=(0,1)[/imath]
Hệ gồm hai trục như vậy gọi là hệ trục Oxy.
Điểm O là gốc tọa độ, Ox gọi là trục hoành, Oy gọi là trục tung.
Với mỗi vectơ [imath]\overrightarrow{u}[/imath] trên mặt phẳng Oxy, có duy nhất cặp số [imath](x_0,y_0)[/imath] sao cho [imath]\overrightarrow{u}=x_0\overrightarrow{i}+y_0\overrightarrow{j}[/imath]. Ta nói vectơ [imath]\overrightarrow{u}[/imath] có tọa độ [imath](x_0,y_0)[/imath] và viết [imath]\overrightarrow{u}=(x_0,y_0)[/imath].
Các số [imath]x_0,y_0[/imath] tương ứng là hoành độ, tung độ của [imath]\overrightarrow{u}[/imath]
Hai vectơ bằng nhau khi chúng có cùng tọa độ
[imath]\overrightarrow{u}(x,y)=\overrightarrow{v}(x',y')\iff \left\{\begin{matrix}x=x'\\y=y'\end{matrix}\right.[/imath]
2. Biểu thức tọa độ của các phép toán vectơ
Cho hai vectơ [imath]\overrightarrow{u}=(x,y)[/imath] và [imath]\overrightarrow{v}=(x',y')[/imath]. Khi đó:
[imath]\overrightarrow{u}+\overrightarrow{v}=(x+x',y+y')[/imath]
[imath]\overrightarrow{u}-\overrightarrow{v}=(x-x',y-y')[/imath]
[imath]k\overrightarrow{u}=(kx,ky)[/imath] với [imath]k\in \mathbb{R}[/imath]
Nếu điểm [imath]M[/imath] có tọa độ [imath](x,y)[/imath] thì [imath]\overrightarrow{OM}=(x,y)[/imath] và độ dài [imath]|\overrightarrow{OM}|=\sqrt{x^2+y^2}[/imath]
Với hai điểm [imath]M(x,y)[/imath] và [imath]N(x',y')[/imath] thì [imath]\overrightarrow{MN}=(x'-x,y'-y)[/imath] và [imath]MN=\sqrt{(x'-x)^2+(y'-y)^2}[/imath]
Luyện tập. Trong mặt phẳng tọa độ Oxy, cho hai điểm [imath]A(2,1); B(3,3)[/imath]
a) Các điểm [imath]O,A,B[/imath] có thẳng hàng không?
b) Tìm điểm [imath]M(x,y)[/imath] để [imath]OABM[/imath] là hình bình hành.
Giải
a) [imath]\overrightarrow{OA}=(2,1); \overrightarrow{OB}=(3,3)[/imath]
Ta có: [imath]\dfrac{2}3\ne \dfrac{1}3[/imath] nên [imath]\overrightarrow{OA}[/imath] không cùng phương với [imath]\overrightarrow{OB}[/imath]. Vậy [imath]O,A,B[/imath] không thẳng hàng
b) [imath]\overrightarrow{MB}=(3-x,3-y)[/imath]
OABM là hình bình hành [imath]\iff \overrightarrow{OA}=\overrightarrow{MB}\iff \left\{\begin{matrix}3-x=2\\3-y=1\end{matrix}\right. \iff x=1, y=2[/imath]