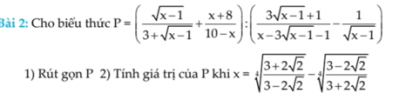[imath]P = \left (\dfrac{x-1}{3 + \sqrt{x-1}} + \dfrac{x +8}{10-x} \right) : \left(\dfrac{3\sqrt{x-1} + 1}{x - 3\sqrt{x-1} - 1} - \dfrac{1}{\sqrt{x-1} }\right)[/imath]
Mọi người giúp em với ạ
songtichcuca)
ĐKXĐ: [imath]\begin{cases} 3 + \sqrt{x -1} \ne 0 \\ x - 1 \ge 0 \\ 10 -x \ne 0 \\ x - 3\sqrt{x -1} - 1 \ne 0 \\ x - 1 \ne 0 \end{cases} \iff ...[/imath]
Đặt [imath]\sqrt{x -1} = a[/imath]
[imath]P = \left (\dfrac{a}{3 + a} + \dfrac{a^2+9}{9-a^2} \right) : \left(\dfrac{3a + 1}{a^2 - 3a} - \dfrac{1}{a} \right)[/imath]
[imath]P = \dfrac{a(3-a) + a^2 + 9}{9-a^2} : \left(\dfrac{3a + 1}{a^2 - 3a} - \dfrac{a-3}{a(a-3)} \right)[/imath]
[imath]P = \dfrac{a(3-a) + a^2 + 9}{9-a^2} :\dfrac{2a+4}{a(a-3)}[/imath]
[imath]P = \dfrac{3(a+3)}{9-a^2}.\dfrac{a(a-3)}{2a+4}[/imath]
[imath]P =\dfrac{-3a}{2a+4} = \dfrac{-3\sqrt{x-1}}{2\sqrt{x-1} + 4}[/imath]
b)
[imath]x = \sqrt[4]{\dfrac{3+2\sqrt{2}}{3-2\sqrt{2}}} - \sqrt[4]{\dfrac{3-2\sqrt{2}}{3+2\sqrt{2}}}[/imath]
[imath]x = \sqrt[4]{(3 + 2\sqrt{2})^2} - \sqrt[4]{(3 - 2\sqrt{2})^2} = \sqrt[4]{(1 + \sqrt{2})^4} - \sqrt[4]{(-1 +\sqrt{2})^4} = 1 + \sqrt{2} + 1 - \sqrt{2} = 2[/imath]
Thay vào ta có: [imath]P = \dfrac{-3}{6} = \dfrac{-1}{2}[/imath]
Có gì không hiểu thì em hỏi lại nha
Ngoài ra, em tham khảo thêm kiến thức tại
Tổng hợp lý thuyết ôn thi HKII lớp 9 | Tổng hợp kiến thức cơ bản toán 9
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
