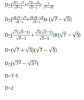[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Bài 1: Rút gọn các biểu thức sau:
4, D = [tex](\frac{\sqrt{21}-\sqrt{7}}{\sqrt{3}-1}+\frac{\sqrt{10}-\sqrt{5}}{\sqrt{2}-1}):\frac{1}{\sqrt{7}-\sqrt{5}}[/tex]
5, E = [tex]21(\sqrt{2+\sqrt{3}}+\sqrt{3-\sqrt{5}})^{2}-6(\sqrt{2-\sqrt{3}}+\sqrt{3+\sqrt{5}})^{2}-15\sqrt{15}[/tex]
Bài 2: Rút gọn các biểu thức sau:
4, D = [tex](\frac{\sqrt{x}}{\sqrt{x}+3}+\frac{3}{\sqrt{x}-3}).\frac{\sqrt{x}+3}{x-9}[/tex]
5, E = [tex](\frac{x}{x+3\sqrt{x}}+\frac{1}{\sqrt{x}+3}) : (1-\frac{2}{\sqrt{x}}+\frac{6}{x+3\sqrt{x}})[/tex]
6, F = [tex]\frac{(\frac{a-b}{\sqrt{a}+\sqrt{b}})^{3}+2a\sqrt{a}+b\sqrt{b}}{3a^{2}+3b\sqrt{ab}}[/tex]
8, H = [tex](\frac{1}{\sqrt{x}-1}-\frac{2}{x-1})(\frac{x+\sqrt{x}}{\sqrt{x}+1}-\frac{1-\sqrt{x}}{\sqrt{x}-x})[/tex]
Bài 3: Cho biểu thức P = [tex](\frac{x-2}{x+2\sqrt{x}}+\frac{1}{\sqrt{x}+2}).\frac{\sqrt{x}+1}{\sqrt{x}-1}[/tex] với x > 0 , x # 1
a) Chứng minh P = [tex]\frac{\sqrt{x}+1}{\sqrt{x}}[/tex]
b) Tìm các giá trị của x để 2P = [tex]2\sqrt{x}+5[/tex]
Bài 4: Chứng minh rằng:
1, [tex]\frac{2+\sqrt{3}}{2+\sqrt{4-2\sqrt{3}}}+\frac{2-\sqrt{3}}{2-\sqrt{4-2\sqrt{3}}}=1[/tex]
2, [tex]\frac{1}{x+\sqrt{x}}+\frac{2\sqrt{x}}{x-1}-\frac{1}{x-\sqrt{x}}=\frac{2}{\sqrt{x}}[/tex]
Bài 5: Chứng minh biểu thức sau không phụ thuộc vào biến:
1, M = [tex]\sqrt{x}+\frac{1}{\sqrt{x}}+\frac{(1-x)(1-\frac{1}{\sqrt{x}})}{1+\sqrt{x}}[/tex], khi x>0
2, P = [tex](\frac{1}{2+2\sqrt{a}}+\frac{1}{2-2\sqrt{a}}-\frac{a^{2}+1}{1-a^{2}})(1+\frac{1}{a})[/tex], với a>0, a#1
4, D = [tex](\frac{\sqrt{21}-\sqrt{7}}{\sqrt{3}-1}+\frac{\sqrt{10}-\sqrt{5}}{\sqrt{2}-1}):\frac{1}{\sqrt{7}-\sqrt{5}}[/tex]
5, E = [tex]21(\sqrt{2+\sqrt{3}}+\sqrt{3-\sqrt{5}})^{2}-6(\sqrt{2-\sqrt{3}}+\sqrt{3+\sqrt{5}})^{2}-15\sqrt{15}[/tex]
Bài 2: Rút gọn các biểu thức sau:
4, D = [tex](\frac{\sqrt{x}}{\sqrt{x}+3}+\frac{3}{\sqrt{x}-3}).\frac{\sqrt{x}+3}{x-9}[/tex]
5, E = [tex](\frac{x}{x+3\sqrt{x}}+\frac{1}{\sqrt{x}+3}) : (1-\frac{2}{\sqrt{x}}+\frac{6}{x+3\sqrt{x}})[/tex]
6, F = [tex]\frac{(\frac{a-b}{\sqrt{a}+\sqrt{b}})^{3}+2a\sqrt{a}+b\sqrt{b}}{3a^{2}+3b\sqrt{ab}}[/tex]
8, H = [tex](\frac{1}{\sqrt{x}-1}-\frac{2}{x-1})(\frac{x+\sqrt{x}}{\sqrt{x}+1}-\frac{1-\sqrt{x}}{\sqrt{x}-x})[/tex]
Bài 3: Cho biểu thức P = [tex](\frac{x-2}{x+2\sqrt{x}}+\frac{1}{\sqrt{x}+2}).\frac{\sqrt{x}+1}{\sqrt{x}-1}[/tex] với x > 0 , x # 1
a) Chứng minh P = [tex]\frac{\sqrt{x}+1}{\sqrt{x}}[/tex]
b) Tìm các giá trị của x để 2P = [tex]2\sqrt{x}+5[/tex]
Bài 4: Chứng minh rằng:
1, [tex]\frac{2+\sqrt{3}}{2+\sqrt{4-2\sqrt{3}}}+\frac{2-\sqrt{3}}{2-\sqrt{4-2\sqrt{3}}}=1[/tex]
2, [tex]\frac{1}{x+\sqrt{x}}+\frac{2\sqrt{x}}{x-1}-\frac{1}{x-\sqrt{x}}=\frac{2}{\sqrt{x}}[/tex]
Bài 5: Chứng minh biểu thức sau không phụ thuộc vào biến:
1, M = [tex]\sqrt{x}+\frac{1}{\sqrt{x}}+\frac{(1-x)(1-\frac{1}{\sqrt{x}})}{1+\sqrt{x}}[/tex], khi x>0
2, P = [tex](\frac{1}{2+2\sqrt{a}}+\frac{1}{2-2\sqrt{a}}-\frac{a^{2}+1}{1-a^{2}})(1+\frac{1}{a})[/tex], với a>0, a#1
