- 24 Tháng mười 2018
- 1,616
- 1,346
- 216
- 24
- TP Hồ Chí Minh
- Đại học Sư phạm Kỹ thuật TP Hồ Chí Minh
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
1. quy tắc xét dấu của nhị thức bậc nhất [imath]ax+b[/imath]
cho nhị thức [imath]ax+b[/imath], để xét dấu của nhị thức thì ta sử dụng quy tắc "trước trái, sau cùng".
khi đó, tập số thực được chia thành 2 khoảng:
trong khoảng [imath]\left ( -\infty;-\frac{b}{a} \right )[/imath] thì nhị thức [imath]ax+b[/imath] trái dấu với a.
trong khoảng [imath]\left ( -\frac{b}{a};+\infty \right )[/imath] thì nhị thức [imath]ax+b[/imath] cùng dấu với a.
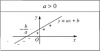
+ với hệ số a>0, ta có đồ thị có dạng như dưới đây:
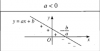
+ với hệ số a<0, ta có đồ thị có dạng như dưới đây:
+ quy tắc xét dấu:
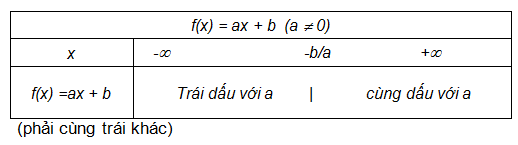
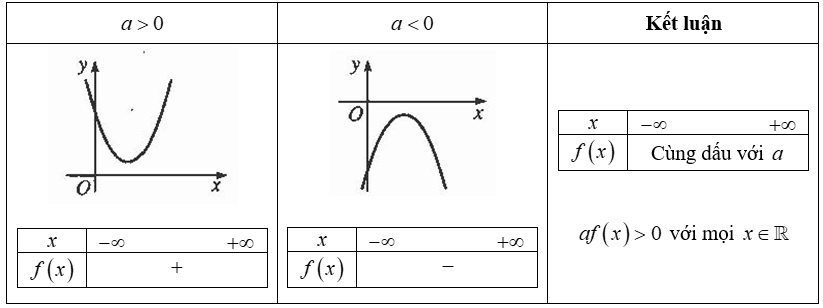
2. quy tắc xét dấu tam thức bậc 2 [imath]ax^2+bx+c[/imath]
Xét dấu tam thức bậc hai [imath]ax^2+bx+c[/imath]
+ Nếu tam thức vô nghiệm thì dấu của nó luôn luôn cùng dấu với hệ số a.
+ Nếu tam thức có nghiệm kép [imath]x_{0}[/imath] thì dấu của nó cũng luôn cùng dấu với hệ số a (trừ trường hợp [imath]x=x_{0}[/imath], khi đó tam thức bằng 0)
Nếu tam thức có nghiệm phân biệt [imath]x_{1}[/imath] và [imath]x_{2}[/imath] ([imath]x_{1}< x_{2}[/imath])
Dùng quy tắc "Trong trái, ngoài cùng" : nằm ngoài khoảng 2 nghiệm thì trái dấu với hệ số a, bên ngoài khoảng 2 nghiêm thì cùng dấu với hệ số a:
Tập số thực được chia thành [imath]3[/imath] khoảng :
Trong khoảng [imath](x_{1};x_{2})[/imath] thì [imath]ax^2+bx+c[/imath] khác dấu với hệ số a
Trong 2 khoảng còn lại thì [imath]ax^2+bx+c[/imath] cùng dấu với hệ số a
3. xét dấu đa thức, phân thức nhanh
để xét dấu một đa thức hay một phân thức nhanh. ta có thể sử dụng quy tắc đan dấu.
+ tìm các nghiệm của nhị thức bậc nhất và tam thức bậc 2,...
+ tính tích các hệ số đi với x mũ cao nhất của từng nhị thức, tam thức,... nếu được giá trị âm, thì khoảng cuối cùng bên phải mang dấu âm và ngược lại, nêu được giá trị dương thì khoảng cuối cùng mang dấu dương.
+ quy tắc đan dấu: qua 1 nghiệm đơn hoặc bội lẻ thì đổi dấu biểu thức, qua nghiệm bội chẵn thì biểu thức không đổi dấu.
ví dụ: xét dấu hàm số sau: [imath]f(x)=(2x-2)(x^2-4x+4)(x^3-9x^2+27x-27)[/imath]
xét các biểu thức trong ngoặc: [imath]\left\{\begin{matrix} 2x-2=0\\ x^2-4x+4=0\\ x^3-9x^2+27x-27=0 \end{matrix}\right.<=>\left\{\begin{matrix} x=1\\ x=2\\ x=3 \end{matrix}\right.[/imath]
tích các hệ số đi với x mũ cao nhất: [imath]2.1.1=2>0[/imath], do đó khoảng cuối cùng phía bên phải mang dấu dương, tức là khoảng [imath]\left ( 3;+\infty \right )[/imath]
nghiệm x=3 là nghiệm bội 3, do đó qua nghiệm này thì biểu thức đổi dấu, tức là biểu thức mang dấu âm trên khoảng [imath](2;3)[/imath]
nghiệm x=2 là nghiệm bội chẵn, do đó qua nghiệm này thì biểu thức không đổi dấu, tức là biểu thức mang dấu âm trên khoảng [imath](1;2)[/imath]
nghiệm x=1 là nghiệm đơn, do đó qua nghiệm này thì biểu thức đổi dấu, tức là biểu thức mang dấu dương trên khoảng [imath](-\infty;1)[/imath]
cho nhị thức [imath]ax+b[/imath], để xét dấu của nhị thức thì ta sử dụng quy tắc "trước trái, sau cùng".
khi đó, tập số thực được chia thành 2 khoảng:
trong khoảng [imath]\left ( -\infty;-\frac{b}{a} \right )[/imath] thì nhị thức [imath]ax+b[/imath] trái dấu với a.
trong khoảng [imath]\left ( -\frac{b}{a};+\infty \right )[/imath] thì nhị thức [imath]ax+b[/imath] cùng dấu với a.
+ với hệ số a>0, ta có đồ thị có dạng như dưới đây:
+ với hệ số a<0, ta có đồ thị có dạng như dưới đây:
+ quy tắc xét dấu:
2. quy tắc xét dấu tam thức bậc 2 [imath]ax^2+bx+c[/imath]
Xét dấu tam thức bậc hai [imath]ax^2+bx+c[/imath]
+ Nếu tam thức vô nghiệm thì dấu của nó luôn luôn cùng dấu với hệ số a.
+ Nếu tam thức có nghiệm kép [imath]x_{0}[/imath] thì dấu của nó cũng luôn cùng dấu với hệ số a (trừ trường hợp [imath]x=x_{0}[/imath], khi đó tam thức bằng 0)
Nếu tam thức có nghiệm phân biệt [imath]x_{1}[/imath] và [imath]x_{2}[/imath] ([imath]x_{1}< x_{2}[/imath])
Dùng quy tắc "Trong trái, ngoài cùng" : nằm ngoài khoảng 2 nghiệm thì trái dấu với hệ số a, bên ngoài khoảng 2 nghiêm thì cùng dấu với hệ số a:
Tập số thực được chia thành [imath]3[/imath] khoảng :
Trong khoảng [imath](x_{1};x_{2})[/imath] thì [imath]ax^2+bx+c[/imath] khác dấu với hệ số a
Trong 2 khoảng còn lại thì [imath]ax^2+bx+c[/imath] cùng dấu với hệ số a
3. xét dấu đa thức, phân thức nhanh
để xét dấu một đa thức hay một phân thức nhanh. ta có thể sử dụng quy tắc đan dấu.
+ tìm các nghiệm của nhị thức bậc nhất và tam thức bậc 2,...
+ tính tích các hệ số đi với x mũ cao nhất của từng nhị thức, tam thức,... nếu được giá trị âm, thì khoảng cuối cùng bên phải mang dấu âm và ngược lại, nêu được giá trị dương thì khoảng cuối cùng mang dấu dương.
+ quy tắc đan dấu: qua 1 nghiệm đơn hoặc bội lẻ thì đổi dấu biểu thức, qua nghiệm bội chẵn thì biểu thức không đổi dấu.
ví dụ: xét dấu hàm số sau: [imath]f(x)=(2x-2)(x^2-4x+4)(x^3-9x^2+27x-27)[/imath]
xét các biểu thức trong ngoặc: [imath]\left\{\begin{matrix} 2x-2=0\\ x^2-4x+4=0\\ x^3-9x^2+27x-27=0 \end{matrix}\right.<=>\left\{\begin{matrix} x=1\\ x=2\\ x=3 \end{matrix}\right.[/imath]
tích các hệ số đi với x mũ cao nhất: [imath]2.1.1=2>0[/imath], do đó khoảng cuối cùng phía bên phải mang dấu dương, tức là khoảng [imath]\left ( 3;+\infty \right )[/imath]
nghiệm x=3 là nghiệm bội 3, do đó qua nghiệm này thì biểu thức đổi dấu, tức là biểu thức mang dấu âm trên khoảng [imath](2;3)[/imath]
nghiệm x=2 là nghiệm bội chẵn, do đó qua nghiệm này thì biểu thức không đổi dấu, tức là biểu thức mang dấu âm trên khoảng [imath](1;2)[/imath]
nghiệm x=1 là nghiệm đơn, do đó qua nghiệm này thì biểu thức đổi dấu, tức là biểu thức mang dấu dương trên khoảng [imath](-\infty;1)[/imath]
Attachments
Last edited by a moderator:
