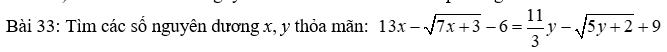KhanhHuyen2006Ta chứng minh bổ đề sau: Nếu [imath]\sqrt{a} -\sqrt{b}=c[/imath] mà [imath]a,b,c[/imath] là số hữu tỉ đồng thời [imath]\sqrt{a},\sqrt{b}[/imath] là số vô tỉ thì [imath]c=0[/imath]
Thật vậy:
Giả sử [imath]c\ne 0[/imath]
[imath]\sqrt{a} =c+ \sqrt{b} \Rightarrow a = c^2+b +2c\sqrt{b} \Rightarrow \sqrt{b} =\dfrac{a-c^2-b}{2c}[/imath] (vô lý do vế trái vô tỉ, vế phải hữu tỉ)
Vậy giả sử sai, bổ đề được chứng minh.
Quay lại bài toán ta có:
[imath]13x-\dfrac{11}{3}y -15 = \sqrt{7x+3} - \sqrt{5y+2}[/imath]
Hiển nhiên vế trái là hữu tỉ, [imath]7x+3,5y+2[/imath] là số hữu tỉ (số nguyên dương luôn)
Nhưng [imath]7x+3[/imath] chia 7 dư 3 nên không phải số chính phương; [imath]5y+2[/imath] chia 5 dư 2 nên cũng không phải số chính phương.
Mà cả 2 đều nguyên dương nên [imath]\sqrt{7x+3} , \sqrt{5y+2}[/imath] là số vô tỉ.
Áp dụng bổ đề suy ra [imath]7x+3=5y+2 \Rightarrow 7x - 14 = 5y -15 \Rightarrow 7(x-2) =5(y-3)[/imath]
Nên khi này, [imath]x = 5m+2; y =7m+3[/imath] với m là số nguyên không âm.
Thay vào giả thiết ta được:
[imath]13(5m+2) - 6 = \dfrac{11}{3} (7m+3)+ 9 \Rightarrow m= 0[/imath]
Vậy [imath]x=2;y=3[/imath] thỏa mãn
Ngoài ra mời em tham khảo:
[Lý thuyết] Chuyên đề HSG: Số học
[Bài tập] Chuyên đề HSG: Số học
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.