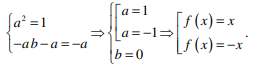@7 1 2 5 Cho em hỏi là mình đồng nhất hệ số như nào vậy ạ?
Thay [imath]\begin{cases} x=1\\ y \in R \end{cases}[/imath] vào [imath](1)[/imath] ta được:
[imath]f(f(y)+1) = y + f(1) (c)[/imath]
Thay [imath]y = -f(1)-1[/imath] vào [imath](c)[/imath] suy ra:[imath]f(f(-f(1)-1)+1)=-1[/imath]
Đặt [imath]a = f(-f(1)-1)+1[/imath] ta được [imath]f(a)=-1[/imath]
Chọn [imath]\begin{cases} y=a\\x \in R\end{cases}[/imath] ta được:
[imath]f(xf(a) + x) = xa + f(x)[imath]
[imath]\overrightarrow xa + f(x) = f(0)[/imath]
Đặt [imath]f(0) = b \overrightarrow f(x) = -ax + b[/imath].
Thế vào [imath](1)[/imath] và đồng nhất hệ số ta được:
[imath]\begin{cases} a^2 = 1\\-ab-a=-a \end{cases}[/imath]
[imath]\overrightarrow \begin{cases} \left[\begin{matrix} a=1\\ a=-1\end{matrix}\right. \\ b = 0 \end{cases}[/imath]
[imath]\rightarrow \left[\begin{matrix} f(x) = x\\ f(x) = -x\end{matrix}\right.[/imath]
Vậy có [imath]2[/imath] hàm số cần tìm là [imath]f(x)=x[/imath] và [imath]f(x) = -x[/imath]
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.