- 24 Tháng mười 2018
- 1,616
- 1,346
- 216
- 24
- TP Hồ Chí Minh
- Đại học Sư phạm Kỹ thuật TP Hồ Chí Minh
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
1. bài toán tham số của mặt cầu cố định tiếp xúc mặt phẳng, đường thẳng.
* Chú ý: (S) tâm I, bán kính r tiếp xúc (P) [tex]<=>r=d(I,(P))[/tex]
(S) tâm I, bán kính r tiếp xúc d [tex]<=>r=d(I,d)[/tex]
- công thức xác định khoảng cách từ điểm tới măt phẳng và đường thẳng.
[tex]I(x_0;y_0;z_0)[/tex] và [tex](P):Ax+By+Cz+D=0[/tex] [tex]=> d(I,(P))=\frac{|Ax_0+By_0+Cz_0+D}{\sqrt{A^2+B^2+C^2}}[/tex]
d qua A, có vector chỉ phương [tex]\overrightarrow{u}[/tex] [tex]=>d(I,d)=\frac{|[\overrightarrow{IA},\overleftarrow{u}]|}{|\overrightarrow{u}|}[/tex]
* mặt cầu tiếp xúc đường thẳng
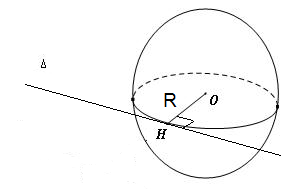
* mặt cầu tiếp xúc mặt phẳng
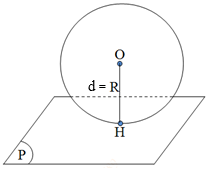
ví dụ 1: [tex]\forall m\in \mathbb{R},(P): (m^2-1)x-2mz-2m+2=0[/tex] luôn tiến xúc một mặt cầu cố định. tìm bán kính của mặt cầu đó.
1 dạng bài toán tuy không khó nhưng lại quá lạ lẫm với nhiều bạn và không biết cách xử lý như thế nào. và đây là cách giải.
gọi [tex]I(a;b;c)[/tex] là tâm của mặt cầu có bán kính là r, khi đó ta sẽ có:
[tex]r=d(I,(P))<=>r=\frac{|(m^2-1)a-2mc-2m+2|}{\sqrt{(m^2-1)^2+(-2m)^2}}<=>r=\frac{|(m^2-1)a-2mc-2m+2|}{m^2+1}[/tex]
vì mặt cầu cố định nên bán kính của mặt cầu là không đổi, vậy nên ta có:
[tex](m^2-1)a-2mc-2m+2=k.(m^2+1)<=>am^2+(-2c-2)m+2=km^2+k[/tex]
đồng nhất hệ số, ta tìm được [tex]\left\{\begin{matrix} k=1\\ a=1\\ c=-1 \end{matrix}\right.[/tex]
do đó, bán kính của mặt cầu là |k|=1.
ví dụ 2: cho [tex]A(2;11;-5);\forall m\in R,(P):2mx+(m^2+1)y+(m^2-1)z-10=0[/tex] luôn tiếp xúc với 2 mặt cầu cố định cùng qua A. tìm bán kính của 2 mặt cầu đó.
khác với ví dụ 1, ví dụ 2 ta cần phải tìm đến 2 mặt cầu. hãy xem lời giải.
giả sử [tex]I(a;b;c)[/tex] tâm của mặt cầu bán kính r.
[tex]r=\frac{|2ma+(m^2+1)b+(m^2-1)c-10|}{\sqrt{4m^2+(m^2+1)^2+(m^2-1)^2}}=\frac{|2ma+(m^2+1)b+(m^2-1)c-10|}{\sqrt{2}(m^2+1)}[/tex]
như ví dụ trên, vì bán kính không đổi nên:
[tex]2ma+(m^2+1)b+(m^2-1)c-10=k\sqrt{2}(m^2+1) <=>(b+c)m^2+2am+b-c-10=k\sqrt{2}m^2+k\sqrt{2}[/tex]
đồng nhất hệ số, ta được: [tex]\left\{\begin{matrix} a=0\\ b=k\sqrt{2}+5\\ c=-5 \end{matrix}\right. =>I(0;k\sqrt{2}+5;-5)[/tex]
khi đó, r=|k|
mà theo đề, mặt cầu đí qua A nên r=IA
<=> [tex]|k|=\sqrt{2^2+(k\sqrt{2}-6)^2}<=>k=2\sqrt{2}\vee k=10\sqrt{2}[/tex]
vậy, bán kính 2 mặt cầu cần tìm là [tex]2\sqrt{2}[/tex] và [tex]10\sqrt{2}[/tex]
2. 2 mặt cầu tiếp xúc
[tex](S_1)[/tex] có tâm [tex]I_1[/tex], bán kính [tex]R_1[/tex]
[tex]S_2[/tex] có tâm [tex]I_2[/tex], bán kính [tex]R_2[/tex]
2 mặt cầu: + tiếp xúc ngoài nếu: [tex]I_1I_2=R_1+R_2[/tex]
+ tiếp xúc trong nếu: [tex]I_1I_2=|R_1-R_2|[/tex]
bài toán: cho (S) tâm I, bán kính R. tìm mặt cầu (S') tiếp xúc (S).
cách giải: + xác định tâm I, bán kính của (S).
+ tìm điểm J cố định sao cho IJ không đổi.
+ mặt cầu cần tìm là (S') có tâm J, bán kính R'.
ví dụ 3: cho mặt cầu (S): [tex](x-a)^2+(y-b)^2+(z-c)^2=9[/tex], với a, b, c thay đổi thỏa mãn [tex]a^2+(b-1)^2+(c-2)^2=25[/tex]. tìm bán kính mặt cầu cố định tiếp xúc với (S).
(S) có [tex]I(a;b;c),R=3[/tex]. đặt [tex]J(0;1;2)[/tex]
theo đề thì [tex]IJ=\sqrt{a^2+(b-1)^2+(c-2)^2}=5[/tex]
vậy mặt cầu (S') có tâm J(0;1;2).
ta có 2 trường hợp tiếp xúc: + tiếp xúc ngoài: [tex]IJ=5=3+R'=>R'=2[/tex]
+ tiếp xúc trong: [tex]IJ=5=|3-R|=>R=8[/tex]
vậy, có 2 mặt cầu tiếp xúc với (S) có bán kính lần lượt là 2 và 8
* Chú ý: (S) tâm I, bán kính r tiếp xúc (P) [tex]<=>r=d(I,(P))[/tex]
(S) tâm I, bán kính r tiếp xúc d [tex]<=>r=d(I,d)[/tex]
- công thức xác định khoảng cách từ điểm tới măt phẳng và đường thẳng.
[tex]I(x_0;y_0;z_0)[/tex] và [tex](P):Ax+By+Cz+D=0[/tex] [tex]=> d(I,(P))=\frac{|Ax_0+By_0+Cz_0+D}{\sqrt{A^2+B^2+C^2}}[/tex]
d qua A, có vector chỉ phương [tex]\overrightarrow{u}[/tex] [tex]=>d(I,d)=\frac{|[\overrightarrow{IA},\overleftarrow{u}]|}{|\overrightarrow{u}|}[/tex]
* mặt cầu tiếp xúc đường thẳng
* mặt cầu tiếp xúc mặt phẳng
ví dụ 1: [tex]\forall m\in \mathbb{R},(P): (m^2-1)x-2mz-2m+2=0[/tex] luôn tiến xúc một mặt cầu cố định. tìm bán kính của mặt cầu đó.
1 dạng bài toán tuy không khó nhưng lại quá lạ lẫm với nhiều bạn và không biết cách xử lý như thế nào. và đây là cách giải.
gọi [tex]I(a;b;c)[/tex] là tâm của mặt cầu có bán kính là r, khi đó ta sẽ có:
[tex]r=d(I,(P))<=>r=\frac{|(m^2-1)a-2mc-2m+2|}{\sqrt{(m^2-1)^2+(-2m)^2}}<=>r=\frac{|(m^2-1)a-2mc-2m+2|}{m^2+1}[/tex]
vì mặt cầu cố định nên bán kính của mặt cầu là không đổi, vậy nên ta có:
[tex](m^2-1)a-2mc-2m+2=k.(m^2+1)<=>am^2+(-2c-2)m+2=km^2+k[/tex]
đồng nhất hệ số, ta tìm được [tex]\left\{\begin{matrix} k=1\\ a=1\\ c=-1 \end{matrix}\right.[/tex]
do đó, bán kính của mặt cầu là |k|=1.
ví dụ 2: cho [tex]A(2;11;-5);\forall m\in R,(P):2mx+(m^2+1)y+(m^2-1)z-10=0[/tex] luôn tiếp xúc với 2 mặt cầu cố định cùng qua A. tìm bán kính của 2 mặt cầu đó.
khác với ví dụ 1, ví dụ 2 ta cần phải tìm đến 2 mặt cầu. hãy xem lời giải.
giả sử [tex]I(a;b;c)[/tex] tâm của mặt cầu bán kính r.
[tex]r=\frac{|2ma+(m^2+1)b+(m^2-1)c-10|}{\sqrt{4m^2+(m^2+1)^2+(m^2-1)^2}}=\frac{|2ma+(m^2+1)b+(m^2-1)c-10|}{\sqrt{2}(m^2+1)}[/tex]
như ví dụ trên, vì bán kính không đổi nên:
[tex]2ma+(m^2+1)b+(m^2-1)c-10=k\sqrt{2}(m^2+1) <=>(b+c)m^2+2am+b-c-10=k\sqrt{2}m^2+k\sqrt{2}[/tex]
đồng nhất hệ số, ta được: [tex]\left\{\begin{matrix} a=0\\ b=k\sqrt{2}+5\\ c=-5 \end{matrix}\right. =>I(0;k\sqrt{2}+5;-5)[/tex]
khi đó, r=|k|
mà theo đề, mặt cầu đí qua A nên r=IA
<=> [tex]|k|=\sqrt{2^2+(k\sqrt{2}-6)^2}<=>k=2\sqrt{2}\vee k=10\sqrt{2}[/tex]
vậy, bán kính 2 mặt cầu cần tìm là [tex]2\sqrt{2}[/tex] và [tex]10\sqrt{2}[/tex]
2. 2 mặt cầu tiếp xúc
[tex](S_1)[/tex] có tâm [tex]I_1[/tex], bán kính [tex]R_1[/tex]
[tex]S_2[/tex] có tâm [tex]I_2[/tex], bán kính [tex]R_2[/tex]
2 mặt cầu: + tiếp xúc ngoài nếu: [tex]I_1I_2=R_1+R_2[/tex]
+ tiếp xúc trong nếu: [tex]I_1I_2=|R_1-R_2|[/tex]
bài toán: cho (S) tâm I, bán kính R. tìm mặt cầu (S') tiếp xúc (S).
cách giải: + xác định tâm I, bán kính của (S).
+ tìm điểm J cố định sao cho IJ không đổi.
+ mặt cầu cần tìm là (S') có tâm J, bán kính R'.
ví dụ 3: cho mặt cầu (S): [tex](x-a)^2+(y-b)^2+(z-c)^2=9[/tex], với a, b, c thay đổi thỏa mãn [tex]a^2+(b-1)^2+(c-2)^2=25[/tex]. tìm bán kính mặt cầu cố định tiếp xúc với (S).
(S) có [tex]I(a;b;c),R=3[/tex]. đặt [tex]J(0;1;2)[/tex]
theo đề thì [tex]IJ=\sqrt{a^2+(b-1)^2+(c-2)^2}=5[/tex]
vậy mặt cầu (S') có tâm J(0;1;2).
ta có 2 trường hợp tiếp xúc: + tiếp xúc ngoài: [tex]IJ=5=3+R'=>R'=2[/tex]
+ tiếp xúc trong: [tex]IJ=5=|3-R|=>R=8[/tex]
vậy, có 2 mặt cầu tiếp xúc với (S) có bán kính lần lượt là 2 và 8
