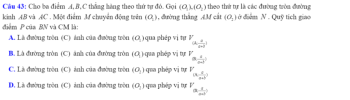Toán 11 Phép vị tự

[nguyenthianh4c]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

Cho [imath]A,B,C[/imath] là [imath]3[/imath] điểm thẳng hàng theo thứ tự đó. Gọi [imath](O_1),(O_2)[/imath] theo thứ tự là các đường tròn đường kính [imath]AB,AC[/imath]. Một điểm [imath]M[/imath] chuyển động trên [imath](O_1)[/imath], đường thẳng [imath]AM[/imath] cắt [imath](O_2)[/imath] tại điểm [imath]N[/imath]. Qũy tích giao điểm [imath]P[/imath] của [imath]BN[/imath] và [imath]CM[/imath] là:
A. Ảnh của đường tròn [imath](O_1)[/imath] qua phép vị tự [imath]V_{(A,\dfrac{a}{a+b})}[/imath]
B. Ảnh của đường tròn [imath](O_1)[/imath] qua phép vị tự [imath]V_{(B,\dfrac{a}{a+b})}[/imath]
C. Ảnh của đường tròn [imath](O_2)[/imath] qua phép vị tự [imath]V_{(A,\dfrac{a}{a+b})}[/imath]
A. Ảnh của đường tròn [imath](O_2)[/imath] qua phép vị tự [imath]V_{(B,\dfrac{a}{a+b})}[/imath]
Anh, chị giải giúp em bài này ạ !!!

 

[7 1 2 5]

[imath]a,b[/imath] ở đây là gì nhỉ vậy bạn.
(Cách làm không cần vẽ hình: Nhận thấy nếu vị tự tâm [imath]A[/imath] thì ảnh của phép vị tự đường tròn [imath](O_1)[/imath] và [imath](O_2)[/imath] đều đi qua [imath]A[/imath].
Mà điểm [imath]P[/imath] không thể trùng [imath]A[/imath] nên loại 2 phương án [imath]A,C[/imath].
Nếu vị tự tâm [imath]B[/imath] thì ảnh của đường tròn [imath](O_1)[/imath] sẽ chứa điểm [imath]B[/imath]. Mà điểm [imath]P[/imath] cũng không trùng [imath]B[/imath] được nên loại [imath]B[/imath].
Vậy chỉ có câu [imath]D[/imath] là đúng.

Nếu còn thắc mắc chỗ nào bạn hãy trả lời dưới topic này để được hỗ trợ nhé. Chúc bạn học tốt ^^
Ngoài ra, bạn tham khảo kiến thức tại topic này nha
Phép dời hình và phép đồng dạng trong mặt phẳng