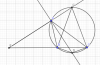
Tam giác ABC có AE là phân giác ngoài tại đỉnh A (E thuộc đường thẳng BC). CMR: AE^2 = EB.EC - AB.AC.
Mn giúp mik vs.
Ta có: $\widehat{EAB}+\widehat{BAD}=\widehat{DAC}+\widehat{CAG}=90^\circ$
Mà $\widehat{BAD}=\widehat{DAC}$
Suy ra $\widehat{EAB}=\widehat{GAC}$
Lại có: $\widehat{ABE}+\widehat{ABC}=180^\circ$
mà $\widehat{AGC}+\widehat{ABC}=180^\circ$
Suy ra $\widehat{ABE}=\widehat{AGC}$
Xét $\Delta ABE$ và $\Delta AGC$ có
$\widehat{ABE}=\widehat{AGC}$
$\widehat{BAE}=\widehat{GAC}$
Suy ra $\Delta ABE\sim \Delta AGC$
$\Rightarrow AB.AC=AG.AE$
$\Delta GBE \sim \Delta CAE$ (g.g)
$\Rightarrow \dfrac{AE}{BE}=\dfrac{EC}{EG}$
$\Rightarrow AE.EG=BE.CE$
$\Rightarrow AE^2=BE.CE-AE.AG=BE.CE-AB.AC$ (đpcm)
Có gì khúc mắc em hỏi lại nhé
Ngoài ra em tham khảo thêm kiến thức tại topic này nhé:
https://diendan.hocmai.vn/threads/on-thi-hk-ham-so-phuong-trinh-luong-giac.844961/
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
