Toán 10 $\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OE}+\overrightarrow{OF}$

[An Na a4k44]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

CÁC BAN GIÚP MK BÀI NÀY VS

 

[hdiemht]

CÁC BAN GIÚP MK BÀI NÀY VSView attachment 86872

___________________________________________
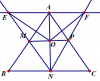
Dễ dàng chứng minh được: $AMNP$ là hình bình hành
[tex]\Rightarrow \left\{\begin{matrix} OA=ON & & \\ OP=OM & & \end{matrix}\right.[/tex]
[tex]\left\{\begin{matrix} OM\parallel AE & & \\ OA=ON & & \end{matrix}\right.\Rightarrow NM=NE[/tex]
Từ đó suy ra: $OM$ là đường trung bình nên [tex]OM=\frac{1}{2}AE\Rightarrow MP=AE[/tex]
CMTT: $MP=AF$
Suy ra: $AE=AF$
Tacó:
[tex]\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OE}+\overrightarrow{OF}=2\overrightarrow{ON}+2\overrightarrow{OA}=2(\overrightarrow{ON}+\overrightarrow{OA})=2\overrightarrow{0}=\overrightarrow{0}[/tex]
Vậy chọn $C$