[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
 Ăn chơi xong rồi, quay lại ôn thi thôi nào các bạn ơi
Ăn chơi xong rồi, quay lại ôn thi thôi nào các bạn ơi HÌNH ĐA DIỆN - KHỐI ĐA DIỆN
Hình đa diện là hình được tạo bởi một số hữu hạn các đa giác thỏa mãn hai tính chất:
i. Hai đa giác phân biệt chỉ có thể hoặc không có điểm chung, hoặc chỉ có một đỉnh chung, hoặc chỉ có một cạnh chung.ii. Mỗi cạnh của đa giác nào cũng là cạnh chung của đúng hai đa giác.
- Mỗi đa giác như trên được gọi là một mặt của hình đa diện.
- Các đỉnh, các cạnh của đa giác ấy theo thứ tự gọi là các đỉnh, các cạnh của hình đa diện.
2. Khái niệm về khối đa diện
- Khối đa diện là phần không gian được giới hạn bởi một hình đa diện, kể cả hình đa diện đó.
- Những điểm không thuộc khối đa diện được gọi là điểm ngoài của khối đa diện. Tập hợp các điểm ngoài được gọi là miền ngoài của khối đa diện.
- Những điểm thuộc khối đa diện nhưng không thuộc hình đa diện ứng với đa diện ấy được gọi là điểm trong của khối đa diện. Tập hợp các điểm trong được gọi là miền trong của khối đa diện.
- Mỗi khối đa diện được xác định bởi một hình đa diện ứng với nó. Ta cũng gọi đỉnh, cạnh, mặt, điểm trong, điểm ngoài… của một khối đa diện theo thứ tự là đỉnh, cạnh, mặt, điểm trong, điểm ngoài… của hình đa diện tương ứng.
- Tên của khối lăng trụ hay khối chóp được đặt theo tên của hình lăng trụ hay chóp giới hạn nó.
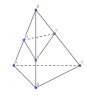
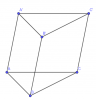
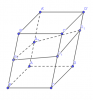
+ Các hình dưới đây là những khối đa diện:
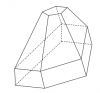
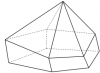
+ Các hình dưới đây không phải là những khối đa diện:
Các em hãy thử giải tích tại sao coi như 1 BT nhỏ nhé
3. Một số kết quả quan trọng
- Một khối đa diện bất kì có ít nhất 4 mặt.
- Mỗi hình đa diện có ít nhất 4 đỉnh.
- Cho $(H)$ là đa diện mà các mặt của nó là những đa giác có $p$ cạnh. Nếu số mặt của $(H)$ là lẻ thì $p$ phải là số chẵn.
- Cho $(H)$ là đa diện có $m$ mặt, mà các mặt của nó là những đa giác có $p$ cạnh. Khi đó số cạnh của $(H)$ là $C=\dfrac{pm}{2}$.
- Mỗi khối đa diện có các mặt là các tam giác thì tổng số các mặt của nó phải là một số chẵn.
- Mỗi khối đa diện bất kì luôn có thể được phân chia được thành những khối tứ diện.
- Mỗi đỉnh của một hình đa diện là đỉnh chung của ít nhất 3 cạnh.
- Nếu khối đa diện có mỗi đỉnh là đỉnh chung của ba cạnh thì số đỉnh phải là số chẵn.
- Mỗi hình đa diện có ít nhất 6 cạnh.
- Không tồn tại hình đa diện có 7 cạnh.
- Với mỗi số nguyên $k\ge 3$ luôn tồn tại một hình đa diện có $2k$ cạnh
- Với mỗi số nguyên $k\ge 4$ luôn tồn tại một hình đa diện có $2k+1$ cạnh
- Không tồn tại đa diện có: số mặt lớn hơn hoặc bằng số cạnh; số đỉnh lớn hơn hoặc bằng số cạnh
- Tồn tại khối đa diện có $2n$ mặt là những tam giác đều.
Khối đa diện được gọi là khối đa diện lồi nếu với bất kì hai điểm $A $ và $B$ nào của nó thì mọi điểm thuộc đoạn thẳng $AB$ cũng thuộc khối đa diện đó.
Lưu ý: Một khối đa diện là khối đa diện lồi khi và chỉ khi miền trong của nó luôn nằm về một phía đối với mỗi mặt phẳng đi qua một mặt của nó.
Công thức Euler: Trong một đa diện lồi nếu gọi $D$ là số đinh, $C$ là số cạnh, $M$ là số mặt thì: D+M=C+2
5. Khối đa diện đều
a. Định nghĩa: Khối đa diện đều là một khối đa diện lồi có hai tính chất sau đây:
- Các mặt là những đa giác đều $n$ cạnh.
- Mỗi đỉnh là đỉnh chung của đúng $p$ cạnh.
Khối đa diện đều như vậy gọi là khối đa diện đều loại $\{n,p\}$.
b. Định lí: Chỉ có 5 khối đa diện đều. Đó là loại $\{3,3\},$ loại $\{4,3\},$ loại $\{3,4\},$ loại $\{5,3\},$ loại $\{3,5\}.$ Tùy theo số mặt của chúng, 5 khối đa diện trên lần lượt có tên gọi là: Khối tứ diện đều, khối lập phương; khối bát diện đều, khối mười hai mặt đều, khối hai mươi mặt đều.
c. Bảng tóm tắt của 5 loại khối đa diện đều
| Khối đa diện đều | Số đỉnh | Số cạnh | Số mặt | Loại |
Tứ diện đều 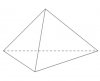 | 4 | 6 | 4 | $\{3,3\}$ |
Khối lập phương 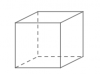 | 8 | 12 | 6 | $\{4,3\}$ |
Bát diện đều 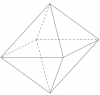 | 6 | 12 | 8 | $\{3,4\}$ |
Mười hai mặt đều  | 20 | 30 | 12 | $\{5,3\}$ |
Hai mươi mặt đều  | 12 | 30 | 20 | $\{3,5\}$ |
Một số kết quả quan trọng
- Cho một khối tứ diện đều. Khi đó
+ Các trọng tâm của các mặt của nó là các đỉnh của một tứ diện đều
+ Các trung điểm của các cạnh của nó là các đỉnh của một khối bát diện đều
+ Các trung điểm của các cạnh của nó là các đỉnh của một khối bát diện đều
- Tâm của các mặt của một khối lập phương là các đỉnh của một bát diện đều
- Tâm của các mặt của một bát diện đều là các đỉnh của một khối lập phương
- Hai đỉnh của một bát diện đều được gọi là hai đỉnh đối diện nếu chúng không cùng thuộc một cạnh của khối đó. Đoạn thẳng nối hai đỉnh đối diện gọi là đường chéo của khối bát diện đều. Khi đó:
+ Ba đường chéo cắt nhau tại trung điểm mỗi đường;
+ Ba đường chéo đôi một vuông góc với nhau;
+ Ba đường chéo bằng nhau.
+ Ba đường chéo đôi một vuông góc với nhau;
+ Ba đường chéo bằng nhau.
Hi vọng topic này sẽ tổng hợp được những kiến thức cần thiết trong quá trình ôn thi của các bạn, chúc các bạn ôn thi thật tốt để dành được kết quả xứng đáng sau 12 năm mài sắt của mình và sau đó là một kì ăn chơi xả láng lunnnn
Topic sẽ tiếp tục được cập nhật, các bạn bấm theo dõi để không bị bỏ lỡ nhé