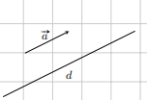- 19 Tháng tám 2018
- 2,749
- 6,038
- 596
- 25
- Thái Bình
- Đại học Y Dược Thái Bình
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
VECTOR TRONG KHÔNG GIAN
1. Định nghĩa
1. Vector là một đoạn thẳng có hướng (có phân biệt điểm đầu và điểm cuối).
2. Vector không là vector có điểm đầu và điểm cuối trùng nhau. Ký hiệu [imath]\overrightarrow{0}[/imath].
3. Ký hiệu vector: [imath]\overrightarrow{AB}[/imath] (điểm đầu là [imath]A[/imath], điểm cuối là [imath]B[/imath] ) hay [imath]\overrightarrow{a} ,\overrightarrow{b} , \overrightarrow{x}, \overrightarrow{y} , . . .[/imath]
4. Độ dài của vector là khoảng cách giữa điểm đầu và điểm cuối của vector đó. Độ dài của [imath]\overrightarrow{AB}[/imath] ký hiệu là [imath]|\overrightarrow{AB}|[/imath], độ dài của [imath]\overrightarrow{a}[/imath] ký hiệu là [imath]|\overrightarrow{a} |[/imath].
5. Giá của vector là đường thẳng đi qua điểm đầu và điểm cuối của vector đó.
6. Hai vector được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.
7. Hai vector bằng nhau là hai vector cùng hướng và có cùng độ dài.
8. Hai vector đối nhau là hai vector ngược hướng nhưng vẫn có cùng độ dài.
9. Các phép toán cộng, trừ, nhân véc-tơ với một số được định nghĩa tương tự trong mặt phẳng.
2. Quy tắc tính toán trong vector
1. Quy tắc ba điểm (với phép cộng): [imath]\overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC}[/imath].
2. Quy tắc ba điểm (với phép trừ): [imath]\overrightarrow{OB} − \overrightarrow{OA} = \overrightarrow{AB}[/imath].
3. Quy tắc ba điểm (mở rộng): [imath]\overrightarrow{AX_1} + \overrightarrow{X_1X_2} + \overrightarrow{X_2X_3} + \cdots + \overrightarrow{X_{n - 1} X_n} + \overrightarrow{X_n B} = \overrightarrow{AB}[/imath]
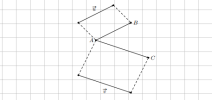
4. Quy tắc hình bình hành:
- [imath]\overrightarrow{AB} + \overrightarrow{AD} = \overrightarrow{AC}[/imath]
- [imath]\overrightarrow{AB} + \overrightarrow{AD} = 2\overrightarrow{AE}[/imath]
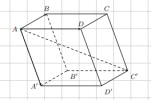
5. Quy tắc hình hộp: [imath]\overrightarrow{AB} +\overrightarrow{AD} +\overrightarrow{AA'} = \overrightarrow{AC'}[/imath] trong đó [imath]ABCD.A'B'C'D'[/imath] là hình hộp
3. Một số hệ thức vector trọng tâm cần nhớ
1. [imath]I[/imath] là trung điểm của đoạn thẳng [imath]AB \iff \overrightarrow{IA} + \overrightarrow{IB} = \overrightarrow{0} \iff \overrightarrow{OA} + \overrightarrow{OB} = 2\overrightarrow{OI}[/imath]
2. [imath]G[/imath] là trọng tâm của tam giác [imath]ABC \iff \overrightarrow{GA}+ \overrightarrow{GB} + \overrightarrow{GC} = \overrightarrow{0} \iff \overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} = 3 \overrightarrow{OG} \iff \overrightarrow{AG} = \dfrac{2}3 \overrightarrow{AM} [/imath] ( với [imath]O[/imath] là một điểm bất kỳ, [imath]M[/imath] là trung điểm cạnh [imath]BC[/imath]
3. [imath]G[/imath] là trọng tâm của tứ diện [imath]ABCD \iff \overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC} + \overrightarrow{GD} = \overrightarrow{0}[/imath]
[imath]\iff \overrightarrow{OA} + \overrightarrow{OB} + \overrightarrow{OC} + \overrightarrow{OD} = 4\overrightarrow{OG} \iff \overrightarrow{AG} = \dfrac{3}4\overrightarrow{AA'}[/imath] ( với [imath]O[/imath] là điểm bất kỳ, [imath]A'[/imath] là trọng tâm của [imath]\triangle BCD[/imath] )
4. [imath]\overrightarrow{a}[/imath] và [imath]\overrightarrow{b} \ne \overrightarrow{0}[/imath] cùng phương [imath]\iff \exists \, k \in \mathbb R \, : \overrightarrow{a} = k \cdot \overrightarrow{b}[/imath]
5. [imath]\overrightarrow{a}[/imath] và [imath]\overrightarrow{b} \ne \overrightarrow{0}[/imath] cùng hướng [imath]\iff \exists \, k \in \mathbb R^+ \, : \overrightarrow{a} = k \cdot \overrightarrow{b}[/imath]
6. [imath]\overrightarrow{a}[/imath] và [imath]\overrightarrow{b} \ne \overrightarrow{0}[/imath] ngược hướng [imath]\iff \exists \, k \in \mathbb R^- \, : \overrightarrow{a} = k \cdot \overrightarrow{b}[/imath]
7. Ba điểm [imath]A, B, C[/imath] thẳng hàng [imath]\iff \exists \, k \in \mathbb R : \overrightarrow{AB} = k \cdot \overrightarrow{AC}[/imath]
4. Điều kiện đồng phẳng của ba vector
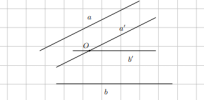
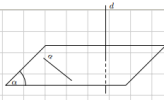
- Định nghĩa 1: Trong không gian, ba vector được gọi là đồng phẳng nếu giá của chúng cùng song song với một mặt phẳng nào đó.
- Hệ quả 1: Nếu có một mặt phẳng chứa vetor này đồng thời song song với giá của hai vector kia thì ba vector đó đồng phẳng.
- Định lí 1: (Điều kiện để ba vector đồng phẳng) Trong không gian cho hai vector [imath]\overrightarrow{a}[/imath] và [imath]\overrightarrow{b}[/imath] không cùng phương và vector [imath]\overrightarrow{c}[/imath] . Khi đó [imath]\overrightarrow{a}, \overrightarrow{b}, \overrightarrow{c}[/imath] đồng phẳng khi và chỉ khi tồn tại cặp số [imath](m; n)[/imath] sao cho [imath]\overrightarrow{c} = m\overrightarrow{a} + n\overrightarrow{b}[/imath] (cặp số [imath](m; n)[/imath] nêu trên là duy nhất).
- Chú ý: Bốn điểm [imath]A,B,C,D[/imath] đồng phẳng [imath]\iff \overrightarrow{AB}, \overrightarrow{AC}, \overrightarrow{AD}[/imath] đồng phẳng [imath]\iff \overrightarrow{AB} = m\overrightarrow{AC} + n\overrightarrow{AD}[/imath]
5. Phân tích một vector theo ba vector không đồng phẳng
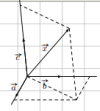
Định lí 2: Cho ba vector [imath]\overrightarrow{a}, \overrightarrow{b}[/imath] và [imath]\overrightarrow{c}[/imath] không đồng phẳng. Với mọi vector [imath]\overrightarrow{x}[/imath], ta đều tìm được duy nhất một bộ số [imath](m; n; p)[/imath] sao cho [imath]\overrightarrow{x}= m\overrightarrow{a} + n \overrightarrow{b}+ p \overrightarrow{c}[/imath]
6. Tích vô hướng của hai vector
1. Nếu [imath]\overrightarrow{a} \ne \overrightarrow{0}[/imath] và [imath]\overrightarrow{b} \ne \overrightarrow{0}[/imath] thì [imath]\overrightarrow{a}\cdot \overrightarrow{b} = |\overrightarrow{a}| \cdot |\overrightarrow{b}| \cdot \cos (\overrightarrow{a}; \overrightarrow{b})[/imath]
2. Nếu [imath]\overrightarrow{a} = \overrightarrow{0}[/imath] hoặc [imath]\overrightarrow{b} = \overrightarrow{0}[/imath] thì [imath]\overrightarrow{a} \cdot \overrightarrow{b} = \overrightarrow{0}[/imath]
3. Bình phương vô hướng của một vector: [imath]\overrightarrow{a}^2 = |\overrightarrow{a}|^2[/imath]