T
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
C
cuphuc13
T
tell_me_goobye
E chả biết thi ĐH khó không
Nhưng cũng post lên 1 số BĐT để tham khảo
3) Cho a, b, c > 0 vàChứng minh rằng

bài này dễ
đặt x=1/a ,.......
\Rightarrowxyz=1
BDT [TEX]\Leftrightarrow 1 + \frac{3}{xy+yz+xz} \geq \frac{6}{x+y+z}[/TEX]
từ [TEX](x+y+z)^2 \geq 3(xy+yz+xz)[/TEX]
nên [TEX] 1+\frac{3}{xy+yz+xz} \geq 1+\frac{9}{(x+y+z)^2}[/TEX]
nên chỉ càn chứng minh
[TEX]1+ \frac{9}{(x+y+z)^2} \geq \frac{6}{x+y+z}[/TEX]
cái này là hằng đẳng thức
hoàn tất
T
tiger3323551
theo AM-GM :
[tex]x\sqrt{3+yz}=\frac{1}{2}2sqrt{x}sqrt{3x+xyz} \le \frac{1}{4}(4x+3x+xyz)[/tex]
tương tự những cái còn lại:
[tex]=>A \le \frac{7}{4}(x+y+z+t)+\frac{1}{4}(xyz+yzt+ztx+txy)=7+\frac{1}{4}(xyz+yzt+ztx+txy)[/tex]
ta chứng minh [tex]xyz+yzt+ztx+txy \le 4[/tex] đẳng thức [tex]x=y=z=t=1[/tex]
thật vậy:
[tex]xy(z+t)+zt(x+y) \le \frac{1}{4}(x+y)^2(z+t)+\frac{1}{4}(z+t)^2(x+y)[/tex]
từ đây có thê => dpcm => max =8
[tex]x\sqrt{3+yz}=\frac{1}{2}2sqrt{x}sqrt{3x+xyz} \le \frac{1}{4}(4x+3x+xyz)[/tex]
tương tự những cái còn lại:
[tex]=>A \le \frac{7}{4}(x+y+z+t)+\frac{1}{4}(xyz+yzt+ztx+txy)=7+\frac{1}{4}(xyz+yzt+ztx+txy)[/tex]
ta chứng minh [tex]xyz+yzt+ztx+txy \le 4[/tex] đẳng thức [tex]x=y=z=t=1[/tex]
thật vậy:
[tex]xy(z+t)+zt(x+y) \le \frac{1}{4}(x+y)^2(z+t)+\frac{1}{4}(z+t)^2(x+y)[/tex]
từ đây có thê => dpcm => max =8
V
vivietnam
G
gaodenvang
H
huycuopbien123
Thtt396
Cho x, y, z dương thoả [tex]x+y+z=3[/tex]. Tìm min
[tex]\frac{x^2}{x+y^2}+\frac{y^2}{y+z^2}+\frac{z^2}{z+x^2}[/tex]
Cho x, y, z dương thoả [tex]x+y+z=3[/tex]. Tìm min
[tex]\frac{x^2}{x+y^2}+\frac{y^2}{y+z^2}+\frac{z^2}{z+x^2}[/tex]
L
lamanhnt
T
tell_me_goobye
Cho x, y, z dương thoả [tex]x+y+z=3[/tex]. Tìm min
[tex]\frac{x^2}{x+y^2}+\frac{y^2}{y+z^2}+\frac{z^2}{z+x^2}[/tex]
BY CAuchy schwarz
[TEX]\sum \frac{x^2}{x+y^2} = \sum \frac{x^4}{x^3+x^2y^2} \geq \frac{(x^2+y^2+z^2)^2}{\sum x^3 +\sum x^2y^2}[/TEX]
cần CM [TEX] 2(\sum x^2)^2 \geq 3(\sum x^2+\sum x^2y^2)[/TEX]
BIẾN ĐỔI p,q,r ta được
BDT trên [TEX]\Leftrightarrow 2(p^2 -2q)^2 \geq 3(p(p^2-3q)+3r+q^2-2pr)[/TEX]
[TEX] \Leftrightarrow 2(9 - 2q)^2 \geq 3(27-9q+3r+q^2-6r) [/TEX]
[TEX] \Leftrightarrow 2(81-36q+4q^2) - 3(27-9q+3r+q^2-6r) \geq 0[/TEX]
[TEX] \Leftrightarrow 81 - 45q+5q^2+9r \geq 0[/TEX]
theo BDT SCHUR [TEX] 9r \geq 4pq -p^3 =12q-27[/TEX]
nên VT [TEX]\geq 81-45q+5q^2+12q-27 =54-33q+5q^2 \geq0[/TEX]
hay [TEX](q-3)(5q-18) \geq 0 [/TEX]
cái này đúng theo BDT schur
HOÀN TẤT
Q
quyenuy0241
Cho x, y, z dương thoả [tex]x+y+z=3[/tex]. Tìm min
[tex]\frac{x^2}{x+y^2}+\frac{y^2}{y+z^2}+\frac{z^2}{z+x^2}[/tex]
Cô si nguợc dấu ra liền
[TEX]\frac{x^2}{x+y^2}=\frac{x(x+y^2)-xy^2}{x+y^2}=x-\frac{xy^2}{x+y^2}\ge x-\frac{y\sqrt{x}}{2}[/TEX]
Các BDT khác tương tự
Cộng vào:
có [tex]A=x+y+z-\frac{y\sqrt{x}+z\sqrt{y}+y\sqrt{z}}{2} [/TEX]
DO [TEX]y\sqrt{x}+z\sqrt{y}+y\sqrt{z} \le \sqrt{(xy+xz+zy)(x+y+z)} \le 3[/TEX]
Vậy [TEX]A \ge \frac{3}{2}[/TEX]
Last edited by a moderator:
M
maituanlinh5409
A
asdasdasdsh
T
tiger3323551
khó nhé:
cho các số thực dương x,y,z chứng minh rằng:
[tex]\frac{x^2+xy}{5x^2+5y^2+2z^2}+\frac{y^2+yz}{5y^2+5z^2+2x^2}+\frac{z^2+zx}{5z^2+5x^2+2y^2} \le \frac{1}{2}[/tex]
cho các số thực dương x,y,z chứng minh rằng:
[tex]\frac{x^2+xy}{5x^2+5y^2+2z^2}+\frac{y^2+yz}{5y^2+5z^2+2x^2}+\frac{z^2+zx}{5z^2+5x^2+2y^2} \le \frac{1}{2}[/tex]
T
tiger3323551
thêm 1 bài toán rất khó:
Cho x,y,z >0 thoả xy+yz+zx=1.Tìm min:
[tex]\frac{1}{sqrt{x^2+yz}}+\frac{1}{sqrt{y^2+xz}}[/tex][tex]+\frac{1}{sqrt{z^2+xy}}[/tex]
Cho x,y,z >0 thoả xy+yz+zx=1.Tìm min:
[tex]\frac{1}{sqrt{x^2+yz}}+\frac{1}{sqrt{y^2+xz}}[/tex][tex]+\frac{1}{sqrt{z^2+xy}}[/tex]
B
bigbang195
thêm 1 bài toán rất khó:
Cho x,y,z >0 thoả xy+yz+zx=1.Tìm min:
[tex]\frac{1}{sqrt{x^2+yz}}+\frac{1}{sqrt{y^2+xz}}[/tex][tex]+\frac{1}{sqrt{z^2+xy}}[/tex]
Dự đoán
Không mất tính tổng quát giả sử
Bài toán đưa về chứng minh
Chuẩn hóa
tương đương
ta lại có
Phép chứng minh hoàn tất
B
bigbang195
khó nhé:
cho các số thực dương x,y,z chứng minh rằng:
[tex]\frac{x^2+xy}{5x^2+5y^2+2z^2}+\frac{y^2+yz}{5y^2+5z^2+2x^2}+\frac{z^2+zx}{5z^2+5x^2+2y^2} \le \frac{1}{2}[/tex]
VT-VP
đến đây đánh giá dễ dàng
B
bigbang195
khó nhé:
cho các số thực dương x,y,z chứng minh rằng:
[tex]\frac{x^2+xy}{5x^2+5y^2+2z^2}+\frac{y^2+yz}{5y^2+5z^2+2x^2}+\frac{z^2+zx}{5z^2+5x^2+2y^2} \le \frac{1}{2}[/tex]
Ta có
Mặt khác theo Cauhy-Schwarz ta lại có:
do vậy
mặt khác do
và
do đó
Ta chỉ cần chứng minh
Lại theo Cauchy-Schwarz ta có
ta lại có
vậy ta có thể viết lại thành:
với
để ý rằng
do đó áp dụng đẳng thức với
Trong đó
chú ý
Mặt khác
BDT được viết lại là
do
hay là
Nếu
Đặt
Từ đó:
BDT hoàn tất dấu bằng xảy ra khi và chỉ khi
B
bigbang195
1 cách khác để chứng minh

ko mất tính tổng quát giả sử
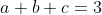
BDT tương đương

Có thể giải bằng AM_GM như sau:
giải sử b nằm giữa a và c thì
(b-c)%20\le%200)
nên:
(b-c)%20=b(a+c)^2)
theo AM-GM
^2=4)
Bài toán được chứng minh xong
ko mất tính tổng quát giả sử
BDT tương đương
Có thể giải bằng AM_GM như sau:
giải sử b nằm giữa a và c thì
nên:
theo AM-GM
Bài toán được chứng minh xong
Last edited by a moderator:

