Toán 10 Ôn tập

[LY LÙN 999]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

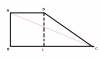
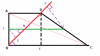
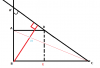
Bài 6: Cho hình thang vuông ABCD, đường cao AB. Biết [tex]\vec{AC}[/tex]. [tex]\vec{AB}[/tex]=[tex]4a^{2}[/tex], [tex]\vec{CA}[/tex].[tex]\vec{CB}[/tex]=[tex]9a^{2}[/tex], [tex]\vec{CB}[/tex].[tex]\vec{CD}[/tex]=[tex]6a^{2}[/tex]
a) Tính các cạnh của hình thang
b) Gọi IJ là đường TB của hình thang, tính độ dài hình chiếu của IJ trên BD
c) Gọi M là điểm trên AC và [tex]\vec{AM}[/tex]=k[tex]\vec{AC}[/tex]. Tính k để BM vuông góc CD

 

[Tạ Đặng Vĩnh Phúc]

a) Em chỉ cần áp dụng chèn điểm cơ bản sẽ có được

$\vec {AC}.\vec {AB} = (\vec{AB}+\vec{BC}).\vec{AB} = AB^2 = 4a^2$
Tương tự: $\vec{CA}.\vec{CB} = 9a^2$ => BC^2 = 9a^2 => BC = 3a
$\vec{CB}. \vec{CD} = 6a^2$ <=> $\vec{CB}.(\vec{CE} + \vec{ED}) = \vec{CB}.\vec{CE} = CB.CE = 6a^2$
mà BC = 3a => CE = 2a =>BE = AB = a;

b)

Em chú ý: IJ = (AD+BC)/2
Ta dễ có: góc INB = góc DBC, và cos INB = cos DBC = BE/BD = $\frac{a}{\sqrt{a^2 + 4a^2}} = \frac{1}{\sqrt{5}}$

Tam giác NII' đồng dạng với NJJ' => $\frac{NI}{NJ} = \frac{I'N}{J'N} <=> \frac{NI}{I'N} = \frac{NJ}{J'N} = \frac{IJ}{I'J'} = \frac{1}{cos INI'} = \frac{1}{cos INB}$
có IJ và INB => I'J' = ...

c)


Ta sẽ đi giải trâu:
$\vec{BM}.\vec{CD} = 0 \Leftrightarrow (\vec{BA}+\vec{AM}).\vec{CD} = 0 = \vec{BA}.\vec{CD} + k\vec{AC}.\vec{CD} = 0$
<=> $AB.CD.cos (CA'B) - k.\vec {CA}.\vec{CD} = 0$
Mà: cos CA'B = sin DCB = EC/CD
$\vec{CA}.\vec{CD} = CA.CD.cos (DCA) = CA.CD.(cos (DCB - ACB)) = CA.CD.(cos (DCB).cos (ACB) + sin (DCB).sin (ACB))$
cos DCB = EC/CD
sin DCB = DE/CD
Tương tự với sin và cos của ACB
Từ đó ta tìm ra k ...