- 27 Tháng mười 2018
- 3,742
- 3,706
- 561
- Hà Nội
- Trường Đại học Bách Khoa Hà Nội
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
*Công thức khai triển Newton:
[tex](a+b)^n=\sum_{k=0}^{n}C_{n}^{k}a^k.b^{n-k}[/tex]
Với a và b là đa thức của x hoặc hằng số.
Dạng 1 ( dễ nhất, thường gặp) : Tìm hệ số của [TEX]x^m[/TEX] theo yêu cầu trong khai triển của [TEX](a+b)^n[/TEX]
Ví dụ: tìm hệ số của [TEX]x^4[/TEX] trong khai triển của [TEX](x^2+1)^{10}[/TEX]
Lời giải: theo công thức khai triển:
[tex](x^2+1)^{10}=\sum_{k=0}^{10}C_{10}^{k}(x^2)^k=\sum_{k=0}^{10}C_{10}^{k}(x^{2k}[/tex]
[TEX]x^4[/TEX] tương ứng với k=2. Vậy hệ số cần tìm là [TEX]C_{10}^{2}[/TEX]
Dạng 2 : Tìm hệ số của [TEX]x^m[/TEX] theo yêu cầu trong khai triển của [TEX](a+b+c)^n[/TEX]
Dạng này phức tạp hơn vì khi khai triển ra xong thì từng số hạng trong đó lại dùng đến khai triển nhị thức tiếp
Ví dụ: Tìm hệ số của số hạng chứa [TEX]x^6[/TEX] trong khai triển của [TEX](3x^2+x+1)^9[/TEX]
Lời giải: theo công thức khai triển:
[tex](3x^2+x+1)^9=\sum_{k=0}^{9}(3x^2+x)^k.1^{9-k}=\sum_{k=0}^{9}(3x^2+x)^k[/tex]
Đến đây: bản thân mỗi số hạng [TEX](3x^2+x)^k[/TEX] ta lại cần dùng khai triển Newton để phá tung nó ra.
Vậy ta sẽ được :
[tex]\sum_{k=0}^{9}C_{9}^{k}(3x^2+x)^k=\sum_{k=0}^{9}.C_{9}^{k}.\sum_{i=0}^{k}C_{k}^{i}.(3x^2)^i.x^{k-i}=\sum_{k=0}^{9}.C_{9}^{k}.\sum_{i=0}^{k}C_{k}^{i}x^{i+k}.3^i[/tex]
Số hạng chứa [TEX]x^6[/TEX] thì [TEX]i+k=6[/TEX] và [TEX]i \leq k[/TEX], do đó ta có các cặp (i;k) thỏa mãn là : (0;6),(1;5) (2;4) (3;3)
Vậy ta có hệ số cần tìm là ( trường hợp ra nhiều cặp giá trị thì hệ số sẽ là cộng dồn tất cả vào) :
[tex]3^0.C_{9}^{6}.C_{6}^{0}+3^1.C_{9}^{5}.C_{5}^{1}+3^2.C_{9}^{4}.C_{4}^{2}+3^3.C_{9}^{3}.C_{3}^{3}=11046[/tex]
Dạng 3: Tìm hệ số lớn nhất trong khai triển đa thức.
Ví dụ: tìm hệ số có giá trị lớn nhất trong khai triển của : [TEX](2x+1)^{13}[/TEX].
Lời giải: [tex](2x+1)^{13}=\sum_{k=0}^{13}C_{13}^{k}.2^k.x^k[/tex]
Vậy các hệ số [TEX]a_k[/TEX] của từng số hạng sẽ là : [TEX]C_{13}^{k}.2^k[/TEX] (với k=0,1,2.....13)
Ta đang nhắm đến hệ số lớn nhất, vậy ta sẽ giải bpt: [TEX]a_k \leq a_{k+1}[/TEX]
<=>[tex]C_{13}^{k}.2^k\leq C_{13}^{k+1}2^{k+1}<=>\frac{13!}{k!.(13-k)!}.2^k\leq \frac{13!}{(k+1)!.(12-k)!}.2^k.2<=>\frac{k+1}{13-k}\leq 2<=>k\leq \frac{25}{3}[/tex]
Do k nguyên, nên với mọi [TEX]k\leq 8[/TEX] (theo bpt giải ở trên) thì ta luôn có [TEX]a_k \leq a_{k+1}[/TEX]
Như vậy trong khoảng k chạy từ 0 đến 8, thì ta có: [TEX]a_0<a_1<a_2<.....<a_8[/TEX]
Vậy [TEX]a_8[/TEX] là hệ số lớn nhất trong khoảng này
Tương tự ta lại cần tiếp tục xem [TEX]a_k>a_{k+1}[/TEX]( tức hệ số của số hạng sau nhỏ hơn hệ số của số hạng trước) khi nào.
Thì rất đơn giản ta đảo chiều của kết quả vừa giải ở trên được là xong: [TEX]k\geq \frac{25}{3}[/TEX]
Vậy với k từ 9 đến 13 thì ta luôn có [TEX]a_9>a_{10}>....>a_{13}[/TEX]
Vậy trong khoảng từ 9 đến 13 thì [TEX]a_9[/TEX] có hệ số lớn nhất
Do vậy ta đã chia làm 2 khoảng, mỗi khoảng ta đã chọn được 1 giá trị lớn nhất, giờ chỉ cần so sánh [TEX]a_8[/TEX] với [TEX]a_9[/TEX] bằng Casio là được.
Ta tính được [TEX]a_8=329472[/TEX], [TEX]a_9=366080[/TEX] vậy hệ số lớn nhất là [TEX]a_9[/TEX]
Đây là cách giải tay, còn quan sát ta sẽ thấy giải mẹo bằng Casio, tuy nhiên hệ số phải bé bé thì máy nó tính mới nhanh. Và do mình không có casio VN570plus nên đây là giả lập của nó. Có lẽ cũng tương tự như thực tế.
Đã biết [TEX]C_{13}^{k}.2^k[/TEX] là hệ số phải không nào? Vậy ta sử dụng mode 7 ( table) để liệt kê toàn bộ dãy ra, đến đâu lớn nhất thì lấy.
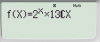
Nhập hàm tương ứng. Xong "=" và "=" , vì không sử dụng đến hàm g(x) nên bỏ qua không nhập
Start thì chọn 0, end thì chọn 13 step là 1, vì k chạy từ 0 đến 13. Rồi nhận được dãy hệ số:
Khi có kết quả ta đã nhận ra ngay k=9 cho hệ số lớn nhất, hoàn toàn đúng với tính toán
[tex](a+b)^n=\sum_{k=0}^{n}C_{n}^{k}a^k.b^{n-k}[/tex]
Với a và b là đa thức của x hoặc hằng số.
Dạng 1 ( dễ nhất, thường gặp) : Tìm hệ số của [TEX]x^m[/TEX] theo yêu cầu trong khai triển của [TEX](a+b)^n[/TEX]
Ví dụ: tìm hệ số của [TEX]x^4[/TEX] trong khai triển của [TEX](x^2+1)^{10}[/TEX]
Lời giải: theo công thức khai triển:
[tex](x^2+1)^{10}=\sum_{k=0}^{10}C_{10}^{k}(x^2)^k=\sum_{k=0}^{10}C_{10}^{k}(x^{2k}[/tex]
[TEX]x^4[/TEX] tương ứng với k=2. Vậy hệ số cần tìm là [TEX]C_{10}^{2}[/TEX]
Dạng 2 : Tìm hệ số của [TEX]x^m[/TEX] theo yêu cầu trong khai triển của [TEX](a+b+c)^n[/TEX]
Dạng này phức tạp hơn vì khi khai triển ra xong thì từng số hạng trong đó lại dùng đến khai triển nhị thức tiếp
Ví dụ: Tìm hệ số của số hạng chứa [TEX]x^6[/TEX] trong khai triển của [TEX](3x^2+x+1)^9[/TEX]
Lời giải: theo công thức khai triển:
[tex](3x^2+x+1)^9=\sum_{k=0}^{9}(3x^2+x)^k.1^{9-k}=\sum_{k=0}^{9}(3x^2+x)^k[/tex]
Đến đây: bản thân mỗi số hạng [TEX](3x^2+x)^k[/TEX] ta lại cần dùng khai triển Newton để phá tung nó ra.
Vậy ta sẽ được :
[tex]\sum_{k=0}^{9}C_{9}^{k}(3x^2+x)^k=\sum_{k=0}^{9}.C_{9}^{k}.\sum_{i=0}^{k}C_{k}^{i}.(3x^2)^i.x^{k-i}=\sum_{k=0}^{9}.C_{9}^{k}.\sum_{i=0}^{k}C_{k}^{i}x^{i+k}.3^i[/tex]
Số hạng chứa [TEX]x^6[/TEX] thì [TEX]i+k=6[/TEX] và [TEX]i \leq k[/TEX], do đó ta có các cặp (i;k) thỏa mãn là : (0;6),(1;5) (2;4) (3;3)
Vậy ta có hệ số cần tìm là ( trường hợp ra nhiều cặp giá trị thì hệ số sẽ là cộng dồn tất cả vào) :
[tex]3^0.C_{9}^{6}.C_{6}^{0}+3^1.C_{9}^{5}.C_{5}^{1}+3^2.C_{9}^{4}.C_{4}^{2}+3^3.C_{9}^{3}.C_{3}^{3}=11046[/tex]
Dạng 3: Tìm hệ số lớn nhất trong khai triển đa thức.
Ví dụ: tìm hệ số có giá trị lớn nhất trong khai triển của : [TEX](2x+1)^{13}[/TEX].
Lời giải: [tex](2x+1)^{13}=\sum_{k=0}^{13}C_{13}^{k}.2^k.x^k[/tex]
Vậy các hệ số [TEX]a_k[/TEX] của từng số hạng sẽ là : [TEX]C_{13}^{k}.2^k[/TEX] (với k=0,1,2.....13)
Ta đang nhắm đến hệ số lớn nhất, vậy ta sẽ giải bpt: [TEX]a_k \leq a_{k+1}[/TEX]
<=>[tex]C_{13}^{k}.2^k\leq C_{13}^{k+1}2^{k+1}<=>\frac{13!}{k!.(13-k)!}.2^k\leq \frac{13!}{(k+1)!.(12-k)!}.2^k.2<=>\frac{k+1}{13-k}\leq 2<=>k\leq \frac{25}{3}[/tex]
Do k nguyên, nên với mọi [TEX]k\leq 8[/TEX] (theo bpt giải ở trên) thì ta luôn có [TEX]a_k \leq a_{k+1}[/TEX]
Như vậy trong khoảng k chạy từ 0 đến 8, thì ta có: [TEX]a_0<a_1<a_2<.....<a_8[/TEX]
Vậy [TEX]a_8[/TEX] là hệ số lớn nhất trong khoảng này
Tương tự ta lại cần tiếp tục xem [TEX]a_k>a_{k+1}[/TEX]( tức hệ số của số hạng sau nhỏ hơn hệ số của số hạng trước) khi nào.
Thì rất đơn giản ta đảo chiều của kết quả vừa giải ở trên được là xong: [TEX]k\geq \frac{25}{3}[/TEX]
Vậy với k từ 9 đến 13 thì ta luôn có [TEX]a_9>a_{10}>....>a_{13}[/TEX]
Vậy trong khoảng từ 9 đến 13 thì [TEX]a_9[/TEX] có hệ số lớn nhất
Do vậy ta đã chia làm 2 khoảng, mỗi khoảng ta đã chọn được 1 giá trị lớn nhất, giờ chỉ cần so sánh [TEX]a_8[/TEX] với [TEX]a_9[/TEX] bằng Casio là được.
Ta tính được [TEX]a_8=329472[/TEX], [TEX]a_9=366080[/TEX] vậy hệ số lớn nhất là [TEX]a_9[/TEX]
Đây là cách giải tay, còn quan sát ta sẽ thấy giải mẹo bằng Casio, tuy nhiên hệ số phải bé bé thì máy nó tính mới nhanh. Và do mình không có casio VN570plus nên đây là giả lập của nó. Có lẽ cũng tương tự như thực tế.
Đã biết [TEX]C_{13}^{k}.2^k[/TEX] là hệ số phải không nào? Vậy ta sử dụng mode 7 ( table) để liệt kê toàn bộ dãy ra, đến đâu lớn nhất thì lấy.
Nhập hàm tương ứng. Xong "=" và "=" , vì không sử dụng đến hàm g(x) nên bỏ qua không nhập
Start thì chọn 0, end thì chọn 13 step là 1, vì k chạy từ 0 đến 13. Rồi nhận được dãy hệ số:
Khi có kết quả ta đã nhận ra ngay k=9 cho hệ số lớn nhất, hoàn toàn đúng với tính toán
