- 20 Tháng chín 2013
- 5,018
- 7,484
- 941
- TP Hồ Chí Minh
- Đại học Bách Khoa TPHCM
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chào mọi người.
Hàng năm ở TPHCM, Kỳ thi HSG Giải toán trên máy tính Casio được tổ chức định kỳ, thu hút các thí sinh tham gia đông đảo.
Là một thí sinh từng dự thi được Giải Nhất, mình đã nghiên cứu qua đề thi các năm và nhận thấy rằng, đề qua các năm không có sự thay đổi nhiều. Nói cách khác, nếu như bạn biết cách làm của các đề năm trước thì khả năng rất cao là năm nay bạn sẽ có giải
Nói vậy thôi, chứ mình không biết đề thi năm nay sẽ ra sau. Nhưng mình viết nên series "MTCT 12" này để chia sẻ những kinh nghiệm, phương pháp chung để giải quyết toàn bộ đề thi từ trước đến nay và hy vọng là nó vẫn sẽ áp dụng được cho năm sau!
Xin gửi tặng đội tuyển Toán 12 trường THPT Tân Thông Hội!
Bài viết này nói về chủ đề hình học...
Các công thức
Có 2 công thức sau bạn cần phải học thêm:
Công thức thứ hai và cách sử dụng hai công thức vào bài hình của các đề thi mình sẽ dành cho 2 bài viết tới nhé.
Định lý Menelaus
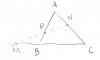
Định lý Menelaus có thể hiểu như sau: Khi ta có ba điểm thẳng hàng $M, N, P$ nằm trên ba cạnh của tam giác $ABC$ thì ta có một hệ thức khá là ngầu như sau:
Ý nghĩa điều này là như sau:
Ví dụ áp dụng
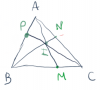
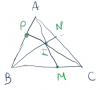
Cho $\dfrac{AP}{AB} = \dfrac{3}4$ và $\dfrac{AN}{AC} = \dfrac{1}{3}$, tính $\dfrac{MB}{MC}$?
Áp dụng định lý Menelaus:
Mẹo ghi nhớ
Để ghi nhớ công thức này, mình thường làm như sau:
Bài tập áp dụng
1. Cho tam giác $ABC$, $N, P$ nằm trên hai cạnh $AC$, $AB$ sao cho $\dfrac{CN}{CA} = \dfrac{7}{8}$ và $\dfrac{AP}{PB} = \dfrac{5}{3}$. Gọi $M$ là giao điểm của $NP$, $BC$. Tính $\dfrac{MB}{MC}$?
2. Cho tam giác $ABC$, $M, N$ nằm trên hai cạnh $BC$, $AC$ sao cho $\dfrac{BM}{MC} = 2$ và $\dfrac{CN}{AN} = 3$. Gọi $I$ là giao điểm của $AM$ và $BN$, $P$ là giao điểm của $CI$ và $AB$.
a) Tính $\dfrac{AI}{AM}$ (gợi ý: tam giác $AMC$)
b) Tính $\dfrac{BI}{BN}$ (gợi ý: $B, M, C$ thẳng hàng trong tam giác $AIN$!)
c) Tính tất cả các tỉ lệ còn lại trong hình.
Đáp số mình sẽ cung cấp trong bài viết tới
Hẹn các bạn tuần sau với công thức $S = 6VR$!
Hàng năm ở TPHCM, Kỳ thi HSG Giải toán trên máy tính Casio được tổ chức định kỳ, thu hút các thí sinh tham gia đông đảo.
Là một thí sinh từng dự thi được Giải Nhất, mình đã nghiên cứu qua đề thi các năm và nhận thấy rằng, đề qua các năm không có sự thay đổi nhiều. Nói cách khác, nếu như bạn biết cách làm của các đề năm trước thì khả năng rất cao là năm nay bạn sẽ có giải
Nói vậy thôi, chứ mình không biết đề thi năm nay sẽ ra sau. Nhưng mình viết nên series "MTCT 12" này để chia sẻ những kinh nghiệm, phương pháp chung để giải quyết toàn bộ đề thi từ trước đến nay và hy vọng là nó vẫn sẽ áp dụng được cho năm sau!
Xin gửi tặng đội tuyển Toán 12 trường THPT Tân Thông Hội!
Bài viết này nói về chủ đề hình học...
Các công thức
Có 2 công thức sau bạn cần phải học thêm:
- Định lý Menelaus
- $S = 6VR$
Công thức thứ hai và cách sử dụng hai công thức vào bài hình của các đề thi mình sẽ dành cho 2 bài viết tới nhé.
Định lý Menelaus
Định lý Menelaus có thể hiểu như sau: Khi ta có ba điểm thẳng hàng $M, N, P$ nằm trên ba cạnh của tam giác $ABC$ thì ta có một hệ thức khá là ngầu như sau:
$\dfrac{MB}{MC} \cdot \dfrac{NC}{NA} \cdot \dfrac{PA}{PB} = 1$
Ý nghĩa điều này là như sau:
- Khi ta có sẵn 2 điểm $N, P$ trên hai cạnh $AB$, $AC$ với các tỉ lệ cố định,
- khi lấy $M$ là giao điểm của $NP$ với cạnh còn lại là $BC$ thì $M$ cũng tạo thành một tỉ lệ cố định trên $BC$.
Ví dụ áp dụng
Cho $\dfrac{AP}{AB} = \dfrac{3}4$ và $\dfrac{AN}{AC} = \dfrac{1}{3}$, tính $\dfrac{MB}{MC}$?
Áp dụng định lý Menelaus:
$\begin{array}{cccccccc}
& \dfrac{MB}{MC} & \cdot & \dfrac{NC}{NA} & \cdot & \dfrac{PA}{PB} &=& 1 \\
\implies & \dfrac{MB}{MC} &\cdot& \dfrac{2}{1}& \cdot &\dfrac{3}{1} &=& 1 \\
\implies & \dfrac{MB}{MC} && && &=& \dfrac{1}6 \end{array}$
& \dfrac{MB}{MC} & \cdot & \dfrac{NC}{NA} & \cdot & \dfrac{PA}{PB} &=& 1 \\
\implies & \dfrac{MB}{MC} &\cdot& \dfrac{2}{1}& \cdot &\dfrac{3}{1} &=& 1 \\
\implies & \dfrac{MB}{MC} && && &=& \dfrac{1}6 \end{array}$
Mẹo ghi nhớ
Để ghi nhớ công thức này, mình thường làm như sau:
- Để ý rằng, các cái tỉ lệ có dạng $\dfrac{\mbox{điểm - đỉnh 1}}{\mbox{điểm - đỉnh 2}}$, trong đó điểm nằm trên đoạn nối từ đỉnh 1 đến đỉnh 2.
Chẳng hạn: $\dfrac{MB}{MC}$, $\dfrac{NA}{NC}$, $\dfrac{PB}{PA}$. Viết $\dfrac{PA}{AB}$ là sai. - Viết cái tỉ lệ cần tính ra, chẳng hạn như ta cần tính tỉ lệ của $P$ thì ta sẽ viết $$\dfrac{PA}{PB}$$
- Dưới mẫu là đỉnh $B$ nên ta sẽ nối tiếp bằng tỉ lệ có chứa đỉnh $B$ trên tử. Ở đây là $\dfrac{MB}{MC}$: $$\dfrac{PA}{PB} \cdot \dfrac{MB}{MC}$$
- Dưới mẫu là đỉnh $C$ nên ta sẽ nối tiếp bằng tỉ lệ có chứa đỉnh $C$ trên tử. Ở đây là $\dfrac{NC}{NA}$: $$\dfrac{PA}{PB} \cdot \dfrac{MB}{MC} \cdot \dfrac{NC}{NA} = 1$$
- Kiểm tra lại, nếu thấy mấy cái đỉnh nối đuôi thành $\dfrac{A}{B} \cdot \dfrac{B}{C} \cdot \dfrac{C}{A} = 1$ thì biểu thức bạn viết là đúng rồi đấy
Tới đây thay số vào nữa là xong.
Bài tập áp dụng
1. Cho tam giác $ABC$, $N, P$ nằm trên hai cạnh $AC$, $AB$ sao cho $\dfrac{CN}{CA} = \dfrac{7}{8}$ và $\dfrac{AP}{PB} = \dfrac{5}{3}$. Gọi $M$ là giao điểm của $NP$, $BC$. Tính $\dfrac{MB}{MC}$?
2. Cho tam giác $ABC$, $M, N$ nằm trên hai cạnh $BC$, $AC$ sao cho $\dfrac{BM}{MC} = 2$ và $\dfrac{CN}{AN} = 3$. Gọi $I$ là giao điểm của $AM$ và $BN$, $P$ là giao điểm của $CI$ và $AB$.
a) Tính $\dfrac{AI}{AM}$ (gợi ý: tam giác $AMC$)
b) Tính $\dfrac{BI}{BN}$ (gợi ý: $B, M, C$ thẳng hàng trong tam giác $AIN$!)
c) Tính tất cả các tỉ lệ còn lại trong hình.
Đáp số mình sẽ cung cấp trong bài viết tới
Hẹn các bạn tuần sau với công thức $S = 6VR$!
Attachments
Last edited: