- 27 Tháng mười 2018
- 3,742
- 3,706
- 561
- Hà Nội
- Trường Đại học Bách Khoa Hà Nội
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Mình sẽ trình bày 1 số khả năng của casio có thể hỗ trợ các bạn làm bài, trong số đó có những cái mà nhiều bạn đã biết. Thì cái gì biết rồi các bạn có thể lướt qua và tìm xem còn gì mình chưa biết hay không.
1. Tính lim/ tìm tiệm cận
Vì bản chất của lim là tính giá trị của hàm số khi x tiến tới gần 1 giá trị nào đó cho trước. Nên ta có thể dùng tính năng CALC để tìm. ( dành cho bạn nào yếu bóng vía, sợ tính tay bị sai )
Ví dụ: tính [tex]\underset{x->0}{lim}\frac{\sqrt{x}}{\sqrt{x+1}-1}[/tex]
Thì ta nhập biểu thức vào:

Sau đó CALC, vì x-> 0 nên ta cho x khá nhỏ xấp xỉ bằng 0, cỡ [TEX]10^{-6}[/TEX] là oke rồi.
Ra kết quả:
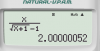
Chú ý: tuy càng nhỏ càng đúng nhưng không cần quá nhỏ, vì máy sẽ làm tròn gây sai, ví dụ CALC với x=[TEX]10^{-15}[/TEX] thì máy làm tròn x=0 luôn, dẫn đến mẫu = 0 , báo Math Error.
2. Solve các nghiệm.
Với pt đơn giản thì không nói, nhưng với pt mũ logarit, mà không biến đổi được do quên công thức hay gì đó. Thì có thể dùng. PT luôn phải nhập vào ở dạng :
[TEX]f(x)[/TEX] . Máy sẽ solve với mặc định vế còn lại bằng 0.
Ví dụ pt: [tex]8^x+9.2^x+\frac{27}{8^x}+\frac{27}{2^x}-64=0[/tex]
Nhập pt vào máy:

Bấm "shift +CALC" . Máy hỏi : x? Ta gán bất kì, mà thường là từ -4 đến 4. Mục đích gán chỉ là giúp máy tìm nghiệm nhanh hơn.
Gán xong ấn "=" 1 lần nữa. Máy trả nghiệm:

Có nghiệm x=0, giờ quay lại nhập biểu thức ban đầu, nhưng chia cho x ( mục đích để tìm giải nghiệm khác 0)

Solve như trên tiếp: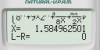
Nghiệm này là [TEX]log_23[/TEX] , dựa vào đáp án có thể chọn được. Với nghiệm xấu thì ta phải gán nghiệm cho biến rồi chia tiếp.
Để gán thì bấm luôn: [TEX]"Alpha X" , "shift RCL A"[/TEX], sau đó chia pt ban đầu cho X(X-A)
Lúc này máy báo "can't solve". Vậy là đã hết nghiệm.
3. Mode "table"
Mode table có thể dùng để dò nghiệm của pt dạng tổ hợp như sau:
Ví dụ: cho [tex]A_{n}^{3}=20n[/tex] , tìm hệ số khai triển của [TEX]x^2[/TEX]
trong khai triển của [TEX](x+3)^n[/TEX]
Vậy mấu chốt là tìm ra n.
Do n nguyên dương nên ta hoàn toàn có thể dùng table để tìm:

Chọn start =3, end =20 , step=1 ( vì dò từng n tăng thêm 1 đơn vị và n>=3)

Được kết quả n=6 là nghiệm của pt.
Ta cũng có thể dùng shift solve để giải pt này, nhưng shift solve cũng có lúc không dò được nghiệm dù pt có nghiệm, nên dùng table thì nhanh hơn!
Dùng table tìm GTLN, GTNN của hàm trên 1 khoảng.
Chỉ dùng với hàm phức tạp, và trên khoảng nhỏ thôi nhé, vì cái này chỉ là tương đối. Các hàm đạo hàm đơn giản thì các bạn nên giải tay
Tìm max của hàm : [tex]\frac{-x^2-x-2}{x+1}[/tex] trong đoạn [0;3]
Nhập hàm vào table.
Chọn Start= 0, End=3, step = (End-Start)/19 = 3/19 (bởi table tính tối đa 20 giá trị). Sau đó xem kết quả:

Thì thấy đây là max. Giá trị max đúng là [tex]1-2\sqrt{2}=-1,828..[/tex]
4. Tổng sigma

Nó là ở cái chỗ log đấy. Về tổng sigma thì ai hiểu bản chất tổng sigma là gì rồi, thì có thể dùng được
Ví dụ ứng dụng: tính tổng 30 số hạng đầu của 1 CSC có U1=1, công sai d=3
Thì ta biết CSC này có dạng: [tex]U_n=1+(n-1).3[/tex] và ta cần tính tổng từ U1 cho tới U30. Vậy ta nhập như sau:

Ngoài ra tổng sigma có thể ứng dụng để giải bài toán VDC bằng cách thử với số nhỏ như mình đã từng nói trong 1 bài viết.
5. Vector
Cái này thì mình không khuyên dùng vì nhập lâu quá, tính tay thì nhanh hơn.
6. Tìm các hệ số trong kết quả tích phân: cái đó thì đừng đầu tư vào vì bộ ra không để mình dò được đâu
1. Tính lim/ tìm tiệm cận
Vì bản chất của lim là tính giá trị của hàm số khi x tiến tới gần 1 giá trị nào đó cho trước. Nên ta có thể dùng tính năng CALC để tìm. ( dành cho bạn nào yếu bóng vía, sợ tính tay bị sai )
Ví dụ: tính [tex]\underset{x->0}{lim}\frac{\sqrt{x}}{\sqrt{x+1}-1}[/tex]
Thì ta nhập biểu thức vào:

Sau đó CALC, vì x-> 0 nên ta cho x khá nhỏ xấp xỉ bằng 0, cỡ [TEX]10^{-6}[/TEX] là oke rồi.
Ra kết quả:

Chú ý: tuy càng nhỏ càng đúng nhưng không cần quá nhỏ, vì máy sẽ làm tròn gây sai, ví dụ CALC với x=[TEX]10^{-15}[/TEX] thì máy làm tròn x=0 luôn, dẫn đến mẫu = 0 , báo Math Error.
2. Solve các nghiệm.
Với pt đơn giản thì không nói, nhưng với pt mũ logarit, mà không biến đổi được do quên công thức hay gì đó. Thì có thể dùng. PT luôn phải nhập vào ở dạng :
[TEX]f(x)[/TEX] . Máy sẽ solve với mặc định vế còn lại bằng 0.
Ví dụ pt: [tex]8^x+9.2^x+\frac{27}{8^x}+\frac{27}{2^x}-64=0[/tex]
Nhập pt vào máy:

Bấm "shift +CALC" . Máy hỏi : x? Ta gán bất kì, mà thường là từ -4 đến 4. Mục đích gán chỉ là giúp máy tìm nghiệm nhanh hơn.
Gán xong ấn "=" 1 lần nữa. Máy trả nghiệm:

Có nghiệm x=0, giờ quay lại nhập biểu thức ban đầu, nhưng chia cho x ( mục đích để tìm giải nghiệm khác 0)

Solve như trên tiếp:

Nghiệm này là [TEX]log_23[/TEX] , dựa vào đáp án có thể chọn được. Với nghiệm xấu thì ta phải gán nghiệm cho biến rồi chia tiếp.
Để gán thì bấm luôn: [TEX]"Alpha X" , "shift RCL A"[/TEX], sau đó chia pt ban đầu cho X(X-A)
Lúc này máy báo "can't solve". Vậy là đã hết nghiệm.
3. Mode "table"
Mode table có thể dùng để dò nghiệm của pt dạng tổ hợp như sau:
Ví dụ: cho [tex]A_{n}^{3}=20n[/tex] , tìm hệ số khai triển của [TEX]x^2[/TEX]
trong khai triển của [TEX](x+3)^n[/TEX]
Vậy mấu chốt là tìm ra n.
Do n nguyên dương nên ta hoàn toàn có thể dùng table để tìm:
Chọn start =3, end =20 , step=1 ( vì dò từng n tăng thêm 1 đơn vị và n>=3)

Được kết quả n=6 là nghiệm của pt.
Ta cũng có thể dùng shift solve để giải pt này, nhưng shift solve cũng có lúc không dò được nghiệm dù pt có nghiệm, nên dùng table thì nhanh hơn!
Dùng table tìm GTLN, GTNN của hàm trên 1 khoảng.
Chỉ dùng với hàm phức tạp, và trên khoảng nhỏ thôi nhé, vì cái này chỉ là tương đối. Các hàm đạo hàm đơn giản thì các bạn nên giải tay
Tìm max của hàm : [tex]\frac{-x^2-x-2}{x+1}[/tex] trong đoạn [0;3]
Nhập hàm vào table.
Chọn Start= 0, End=3, step = (End-Start)/19 = 3/19 (bởi table tính tối đa 20 giá trị). Sau đó xem kết quả:

Thì thấy đây là max. Giá trị max đúng là [tex]1-2\sqrt{2}=-1,828..[/tex]
4. Tổng sigma

Nó là ở cái chỗ log đấy. Về tổng sigma thì ai hiểu bản chất tổng sigma là gì rồi, thì có thể dùng được
Ví dụ ứng dụng: tính tổng 30 số hạng đầu của 1 CSC có U1=1, công sai d=3
Thì ta biết CSC này có dạng: [tex]U_n=1+(n-1).3[/tex] và ta cần tính tổng từ U1 cho tới U30. Vậy ta nhập như sau:

Ngoài ra tổng sigma có thể ứng dụng để giải bài toán VDC bằng cách thử với số nhỏ như mình đã từng nói trong 1 bài viết.
5. Vector
Cái này thì mình không khuyên dùng vì nhập lâu quá, tính tay thì nhanh hơn.
6. Tìm các hệ số trong kết quả tích phân: cái đó thì đừng đầu tư vào vì bộ ra không để mình dò được đâu

