- 14 Tháng năm 2017
- 3,974
- 7,627
- 744
- 23
- Phú Yên
- Trường THPT Lương Văn Chánh
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
MỘT SỐ PHƯƠNG PHÁP GIẢI MẠCH ĐIỆN KHÔNG ĐỔI
Chắc hẳn nhiều bạn đã quá chán ngán với việc sử dụng định luật Ôm để giải mạch điện rồi đúng không nào. Chính vì vậy, mình sẽ giới thiệu các bạn thêm một số phương pháp giải mạch điện để các bạn có thể áp dụng trong một số bài toán phức tạp và cũng có thể dùng để “thể hiện” trước bạn bè Mình xin phép được sử dụng 3 mạch điện ở trong topic này để làm ví dụ (để các bạn có thể dễ dàng so sánh các phương pháp).
Mình sẽ giới thiệu 4 phương pháp sau:
1) Phương pháp sử dụng định luật Ôm.
2) Phương pháp sử dụng định luật Kiếc-xốp (Kirchhoff).
3) Phương pháp nguồn tương đương.
4) Phương pháp chồng chập.
Chúng ta cùng đi vào tìm hiểu về các phương pháp này nhé
1) Phương pháp sử dụng định luật Ôm.
Phương pháp này đã được đề cập và cũng rất chi tiết nên mình chỉ tóm tắt lại các bước để giải mạch điện bằng định luật Ôm:
- Bước 1: Quy ước chiều dòng điện, đặt ẩn dòng điện.
- Bước 2: Viết các phương trình định luật Ôm.
- Bước 3: Tổng hợp hiệu điện thế.
- Bước 4: Giải hệ phương trình.
2) Phương pháp sử dụng định luật Kiếc-xốp (Kirchhoff).
Đây có lẽ là một phương pháp mới đối với nhiều bạn đúng không nào. Trước khi đi vào phương pháp chúng ta cần chuẩn bị một chút kiến thức nhé!!!
a) Định luật Kiếc-xốp I: Tổng đại số những cường độ dòng điện đi qua một nút phải bằng 0.
Biểu diễn toán học: $\sum {I_k} = 0 $
Một cách đơn giản thì định luật này có nghĩa là tổng cường độ các dòng điện đi vào một nút phải bằng tổng cường độ các dòng điện đi ra nút đó. Quy ước là dòng điện đi vào nút sẽ có dấu "+" còn đi ra sẽ có dấu "-".
Ví dụ:
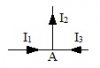
Xét nút A thì ta có $I_1 + I_3 - I_2 = 0$, hay $I_1 + I_3 = I_2$
b) Định luật Kiếc-xốp II: Trong một mắt bất kì, tổng đại số các suất điện động trong mắt đó bằng tổng đại số các độ giảm điện thế trên các đoạn mạch không phân nhánh thuộc mắt đó.
Biểu diễn toán học: $\sum{E_k} = \sum{I_k.R_k}$
Hiểu đơn giản thì tổng các tích của điện trở và dòng điện đi qua nó trong một mạch kín sẽ bằng tổng các suất điện động có trong mắt đó. Để làm vậy thì trước đó chúng ta cần quy ước một chiều đường đi $f$ trong mắt. Dòng điện cùng chiều với chiều của đường đi sẽ có dấu “+”, ngược lại sẽ mang dấu “-“. Nguồn điện mà có chiều từ cực âm sang cực dương trùng với chiều của f thì mang dấu “+”, ngược lại sẽ mang dấu “-“.
Ví dụ:
Khi xét mắt mạch ở trên, ta có: $-I_1R_1+I_2R_2 = E_1+E_2$
Cho những ai đọc 2 định luật trên mà chưa hiểu "nút" với "mắt mạch" là gì.

- Nút là nơi giao nhau của các dòng điện khác nhau. Trong quá trình giải chúng ta có thể đặt thêm các điểm khác trên mạch và cũng có thể gọi chúng là một nút, nhưng khá ít người làm vậy.
- Mắt mạch (có thể gọi là mắt) là một đoạn mạch điện kín. Các dòng điện trong mạch này có thể không thống nhất về chiều lẫn độ lớn, nhưng chỉ cần là một vòng mạch kín thì ta sẽ gọi đó là mắt mạch.
- Ví dụ:
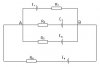
- Ở đoạn mạch trên thì $A, B$ được gọi là nút, các đoạn mạch $AE_1BE_2A, AE_2BE_4A...$ được gọi là những mắt mạch.
- Bước 0: Quy ước chiều đường đi của mắt.
- Bước 1: Quy ước chiều dòng điện, đặt ẩn dòng điện.
- Bước 2: Áp dụng định luật Kiếc-xốp.
- Bước 3: Giải hệ phương trình.

Bước 0: Quy ước chiều đường đi cho các mắt trong mạch.
Việc quy ước này thực chất để phục vụ việc xét dấu của các đại lượng trong mạch (suất điện động, cường độ dòng điện...). Chúng ta sẽ vẽ một cung tròn trong mạch và quy định chiều dương của nó. Ví dụ thế này:
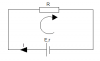
Trong hình trên thì chiều đường đi sẽ là chiều ngược chiều kim đồng hồ. Định luật Kiếc-xốp II được viết như sau: $E=I.R+I.r$ (Vì I cùng chiều dương và chiều từ cực âm đến cực dương của nguồn cũng cùng với chiều dương).
Tuy nhiên, để cho đồng bộ và khỏi mất thời gian suy nghĩ nhiều trong quá trình giải mạch thì ta thường quy ước chiều đường đi là chiều ngược chiều kim đồng hồ. Vì việc quy ước sẽ không ảnh hưởng nhiều đến việc tính toán nên ta không cần phải dành quá nhiều thời gian cho bước này. Lí do mình để nó là bước 0 vì chúng ta đã quy ước sẵn và trong thực hành có thể bỏ qua bước này.
Bước 1: Quy ước chiều dòng điện trong mạch, đặt ẩn dòng điện.
Việc quy ước chiều dòng điện phụ thuộc vào mỗi người sao cho bạn cảm thấy việc tính toán đơn giản nhất.
Ví dụ:
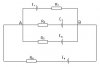
Ở mạch điện này thì chúng ta có thể có rất nhiều cách để quy ước chiều các dòng điện.
Có thể là thế này
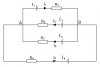
Hoặc thế này
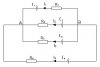
Nếu bạn không quan tâm đến việc hệ phương trình có dễ giải hay không thì có thể quy ước chiều dòng điện theo một chiều duy nhât (chiều từ trái sang phải hoặc từ phải sang trái cho tất cả các nhánh). Nên mình thường sẽ quy ước giống với hình thứ 2.
Việc đặt ẩn thì ta sẽ đặt cho mỗi dòng điện là một ẩn và chúng ta chỉ giải hệ các dòng điện. Việc này sẽ giúp làm giảm thời gian chúng ta khi xem xét phải đặt ẩn như thế nào.
Ví dụ như mạch điện phía trên, chúng ta đặt ngay 4 ẩn dòng điện là $I_1,I_2,I_3,I_4$.
Bước 2: Sử dụng 2 định luật Kiếc-xốp để lập các phương trình.
Gọi số ẩn đặt ở bước 2 là $n$. Nếu trong mạch có $m$ nút thì dựa vào định luật Kiếc-xốp I ta viết $m - 1$ phương trình, dựa vào định luật Kiếc-xốp II ta viết thêm $n – (m-1)$ phương trình còn lại.
Áp dụng cho mạch điện phía trên.
+ Có 2 nút (A và B) nên ta sẽ viết 2-1 = 1 phương trình từ định luật I.
- Xét nút A: $I_1+I_2+I_3 + I_4 = 0$ (4 dòng điện đều đi vào nút A)
- Xét mắt $AE_1BE_2A:$ $I_1R_1-I_2R_2=E_1+E_2$
- Xét mắt $AE_1BE_3A:$ $I_1R_1-I_3R_3=E_1+E_3$
- Xét mắt $AE_1BE_4A:$ $I_1R_1-I_4R_4=E_1+E_4$
Khi đã có hệ phương trình thì ta chỉ việc tiến hành giải nó và kết luận.
*Lưu ý: Tương tự phương pháp giải mạch bằng định luật Ôm, nếu giá trị đại số của dòng điện là âm thì dòng điện đó sẽ có chiều ngược lại so với quy ước và có độ lớn bằng giá trị tuyệt đối của giá trị tìm được.
Cùng đi vào một ví dụ cụ thể để áp dụng nào!!!
Ví dụ 1:

Bước 0: Theo như quy ước ở trên thì chiều của các mắt trong mạch là ngược chiều kim đồng hồ. Ở các ví dụ khác mình sẽ bỏ qua bước này.
Bước 1: Quy ước chiều dòng điện trong mạch, đặt ẩn dòng điện.
Vì không có dòng điện qua AB nên ta giả sử chiều của dòng như sau:
Lưu ý là ở đây chỉ có 1 dòng điện (vì không có dòng qua AB) nên ta phải quy ước cho đồng bộ.
Chúng ta có 1 dòng điện nên ta đặt 1 ẩn dòng điện là $I$
(Ngoài ra chúng ta có thể xem $A,B$ là 2 mắt và đặt 2 ẩn dòng điện là $I_1,I_2$, chiều bất kỳ)
Bước 2: Áp dụng 2 định luật Kiếc-xốp.
Vì ở đây chúng ta chỉ có 1 mắt nên ta áp dụng luôn định luật Kiếc-xốp II:
- $E_1-E_2-E_3 = IR_1+IR_2+Ir_1+Ir_2+Ir_3$
Bước 3: Giải hệ phương trình.
Ở đây ta chỉ có 1 phương trình nên ngay lập tức giải được $I = -10/9(A)$. Ta thấy $I < 0$ nên chiều dòng điện giả sử là sai, chiều đúng sẽ là chiều ngược lại.
Số chỉ vôn kế chính là hiệu điện thế $U_{AB}$.
Mà $U_{AB} = E_3+I(R_2+r_3) = 12-10/9 . 6 = 28/9(V)$
Ví dụ 2:
Giải
Bước 1: Quy ước chiều dòng điện, đặt ẩn dòng điện.Ta giả sử chiều dòng điện trong mạch như sau:
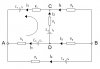
Ta sẽ đặt 6 ẩn dòng điện $I_1,I_2,I_3,I_4,I_5,I_6$
Bước 2: Áp dụng 2 định luật Kiếc-xốp.
Ta có 4 nút, vậy sẽ có 4-1=3 phương trình từ định luật I:
- Nút A: $I_1+I_3+I_4=0$ .
- Nút B: $-I_4-I_5-I_6=0$ .
- Nút C: $I_2+I_6-I_1=0$ .
- Mắt $ACBA: E_1-E_2+E_3=I_1.(r_1+R_1)+I_2.(r_2+R_2)-I_3.(r_3+R_3)$ .
- Mắt $DCBD: E_2 = -I_2.(r_2+R_2)-I_5.R_5+I_6.R_6$ .
- Mắt $ABE_4A: -E_3+E_4=I_3.(r_3+R_3)-I_4.(r_4+R_4)+I_5R_5$ .
- $I_1+I_3+I_4=0$ .
- $-I_4-I_5-I_6=0$ .
- $I_2+I_6-I_1=0$ .
- $3I_1+5I_2-5I_3 = 8$ .
- $-5I_2-8I_5+8I_6 = 6$ .
- $5I_3-7I_4+8I_5 = 0$ .
Bước 3: Giải hệ phương trình. Đến đoạn này thì mình lười rồi, nhờ các bạn vậy
*Chú ý: Phương pháp này sẽ rất hiệu quả trong việc tìm dòng điện đối với các mạch phức tạp, có nhiều nhánh khi hệ phương trình chính chỉ gồm các phương trình liên quan đến dòng điện.
Last edited: