- 27 Tháng mười 2018
- 3,742
- 3,705
- 561
- Hà Nội
- Trường Đại học Bách Khoa Hà Nội
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Dạng 1: Viết ptmp (P) chứa đường thẳng d và cách điểm M một khoảng lớn nhất.
Dạng này khá là quen thuộc rồi, mình chỉ nêu lại thôi.
Gọi K là hình chiếu vuông góc của M lên d => K cố định.
Gọi H là hình chiếu của M lên (P) => MH vuông HK
=> [TEX]MH \leq MK[/TEX] => MH lớn nhất khi H trùng K.
Vậy bài toán trở thành viết ptmp (P) qua K và vuông góc MK.
Dạng 2: Viết ptdt d đi qua điểm A nằm trong mp (P) cho trước, và cách điểm M (nằm ngoài (P), AM không vuông góc với (P)), một khoảng nhỏ nhất ( lớn nhất )
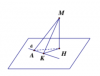
*Trường hợp nhỏ nhất:
Gọi H là hình chiếu của M lên (P), tìm tọa độ H => H cố định
Gọi K là hình chiếu vuông góc của M lên d.
Ta luôn có : [TEX]MK \geq MH[/TEX]=> MK min khi K trùng H.
Vậy bài toán trở thành viết pt d qua A và H
*Trường hợp lớn nhất:
Ta luôn có :
[TEX]MK \leq MA[/TEX]=>MK max khi K trùng A=> d là đường thẳng qua A và vuông AM
Để viết pt của d ta có: [TEX]u_d=[n_P;AM][/TEX]
Có vtcp và điểm đi qua là A thì viết được pt của d
Dạng 3: Viết ptmp (P) chứa đường thẳng d, và tạo với d' một góc lớn nhất.
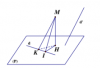
Lấy K thuộc d, dựng KM // d' . Gọi H là hình chiếu của M lên (P).
Ta có góc giữa d' và (P) là góc giữa MK và (P) , hay góc MKH.
Gọi I là hình chiếu của M lên d. Ta có:
[TEX]sinMKH=MH/MK \leq MI/MK[/TEX]
Để góc MKH là max thì [TEX]sinMKH[/TEX] max, khi đó H trùng I
Vậy bài toán trở thành: Viết ptmp (P) chứa d và vuông góc với MI.
Tất nhiên, nếu giải : chọn K bất kì thuộc d, chọn M bất kì sao cho MK//d' , sau đó tìm hình chiếu I của M lên d, và viết pt. Giải như vậy là khá dài. Vậy ta để ý: (MKI) chứa d và có MK // d' nên (MKI) // d'.
Mà (MKI) có MI vuông góc (P) nên (MKI) vuông góc (P) .
Vậy (P) có 1 vtcp là vtpt của (MKI) , vtcp còn lại của (P) là vtcp của d, vì d nằm trong (P).
Tổng kết ta có: [TEX]n_P=[ [u_d;u_{d'}];u_d][/TEX] , là tích có hướng của [TEX]u_d,u_{d'}[/TEX] nhân tiếp có hướng với [TEX]u_d[/TEX]. Đây là công thức chốt cho ai nhớ tốt có thể thuộc luôn, nếu gặp thì dùng.
Ví dụ: Viết ptmp (P) chứa d: [tex]\frac{x-1}{2}=\frac{y-1}{3}=\frac{z-2}{2}[/tex] và tạo với đường thẳng d':
[tex]\frac{x-1}{3}=\frac{y-2}{2}=\frac{z-4}{2}[/tex] một góc lớn nhất.
Giải: Ta có : [TEX]u_d=(2;3;2), u_{d'}=(3;2;2)[/TEX]
=>[TEX]n_P=[[u_d;u_{d'}];u_d]=(19;-14;2)[/TEX]
A(1;1;2) thuộc d nên thuộc (P)
=> pt của (P) là: 19(x-1)-14(y-1)+2(z-2)=0
Dạng 4: Cho mp (P) và điểm A thuộc (P) và đường thẳng d ( d cắt (P) và không vuông góc với (P)). Viết pt đường thẳng d' đi qua A, nằm trong (P) và tạo với d một góc nhỏ nhất.
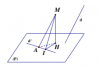
Trông có vẻ vẫn khá tương tự hình của dạng 3, chỉ có điều giờ d và d' đổi chỗ cho nhau. Việc dưng hình thì vẫn tương tự. Ta có góc giữa d và d' là góc MAI . Ta có:
[TEX]cosMAI=AI/MA[/TEX]
Để góc MAI là min thì [TEX]cosMAI [/TEX] đạt max. [TEX]CosMAI [/TEX]max khi AI max hay AI = AH hay I trùng H.
Nhận thấy: MA//d mà H là hình chiếu của M lên (P) nên AH song song với hình chiếu của d lên (P)
Vậy bài toán trở thành: Viết pt d' nằm trong (P), đi qua A và song song với hình chiếu của d lên (P).
Ta có : d'//AH nên d' vuông góc với tích có hướng của [TEX][n_P,u_d][/TEX]
d' nằm trong (P) nên d' vuông góc với vtpt [TEX]n_P[/TEX]
Vậy kết quả cuối cùng thu được: [TEX]u_{d'}=[[n_P;u_d];n_P][/TEX]
Có vtcp, có điểm đi qua ( là A) , ta có thể viết được pt của d' rồi.
Trên đây là 1 số dạng nhỏ, tất nhiên đề bài có thể biến tấu đi, chúng ta phải tưởng tượng một chút để có thể vẽ hình và tìm ra hướng giải!
Dạng này khá là quen thuộc rồi, mình chỉ nêu lại thôi.
Gọi K là hình chiếu vuông góc của M lên d => K cố định.
Gọi H là hình chiếu của M lên (P) => MH vuông HK
=> [TEX]MH \leq MK[/TEX] => MH lớn nhất khi H trùng K.
Vậy bài toán trở thành viết ptmp (P) qua K và vuông góc MK.
Dạng 2: Viết ptdt d đi qua điểm A nằm trong mp (P) cho trước, và cách điểm M (nằm ngoài (P), AM không vuông góc với (P)), một khoảng nhỏ nhất ( lớn nhất )
*Trường hợp nhỏ nhất:
Gọi H là hình chiếu của M lên (P), tìm tọa độ H => H cố định
Gọi K là hình chiếu vuông góc của M lên d.
Ta luôn có : [TEX]MK \geq MH[/TEX]=> MK min khi K trùng H.
Vậy bài toán trở thành viết pt d qua A và H
*Trường hợp lớn nhất:
Ta luôn có :
[TEX]MK \leq MA[/TEX]=>MK max khi K trùng A=> d là đường thẳng qua A và vuông AM
Để viết pt của d ta có: [TEX]u_d=[n_P;AM][/TEX]
Có vtcp và điểm đi qua là A thì viết được pt của d
Dạng 3: Viết ptmp (P) chứa đường thẳng d, và tạo với d' một góc lớn nhất.
Lấy K thuộc d, dựng KM // d' . Gọi H là hình chiếu của M lên (P).
Ta có góc giữa d' và (P) là góc giữa MK và (P) , hay góc MKH.
Gọi I là hình chiếu của M lên d. Ta có:
[TEX]sinMKH=MH/MK \leq MI/MK[/TEX]
Để góc MKH là max thì [TEX]sinMKH[/TEX] max, khi đó H trùng I
Vậy bài toán trở thành: Viết ptmp (P) chứa d và vuông góc với MI.
Tất nhiên, nếu giải : chọn K bất kì thuộc d, chọn M bất kì sao cho MK//d' , sau đó tìm hình chiếu I của M lên d, và viết pt. Giải như vậy là khá dài. Vậy ta để ý: (MKI) chứa d và có MK // d' nên (MKI) // d'.
Mà (MKI) có MI vuông góc (P) nên (MKI) vuông góc (P) .
Vậy (P) có 1 vtcp là vtpt của (MKI) , vtcp còn lại của (P) là vtcp của d, vì d nằm trong (P).
Tổng kết ta có: [TEX]n_P=[ [u_d;u_{d'}];u_d][/TEX] , là tích có hướng của [TEX]u_d,u_{d'}[/TEX] nhân tiếp có hướng với [TEX]u_d[/TEX]. Đây là công thức chốt cho ai nhớ tốt có thể thuộc luôn, nếu gặp thì dùng.
Ví dụ: Viết ptmp (P) chứa d: [tex]\frac{x-1}{2}=\frac{y-1}{3}=\frac{z-2}{2}[/tex] và tạo với đường thẳng d':
[tex]\frac{x-1}{3}=\frac{y-2}{2}=\frac{z-4}{2}[/tex] một góc lớn nhất.
Giải: Ta có : [TEX]u_d=(2;3;2), u_{d'}=(3;2;2)[/TEX]
=>[TEX]n_P=[[u_d;u_{d'}];u_d]=(19;-14;2)[/TEX]
A(1;1;2) thuộc d nên thuộc (P)
=> pt của (P) là: 19(x-1)-14(y-1)+2(z-2)=0
Dạng 4: Cho mp (P) và điểm A thuộc (P) và đường thẳng d ( d cắt (P) và không vuông góc với (P)). Viết pt đường thẳng d' đi qua A, nằm trong (P) và tạo với d một góc nhỏ nhất.
Trông có vẻ vẫn khá tương tự hình của dạng 3, chỉ có điều giờ d và d' đổi chỗ cho nhau. Việc dưng hình thì vẫn tương tự. Ta có góc giữa d và d' là góc MAI . Ta có:
[TEX]cosMAI=AI/MA[/TEX]
Để góc MAI là min thì [TEX]cosMAI [/TEX] đạt max. [TEX]CosMAI [/TEX]max khi AI max hay AI = AH hay I trùng H.
Nhận thấy: MA//d mà H là hình chiếu của M lên (P) nên AH song song với hình chiếu của d lên (P)
Vậy bài toán trở thành: Viết pt d' nằm trong (P), đi qua A và song song với hình chiếu của d lên (P).
Ta có : d'//AH nên d' vuông góc với tích có hướng của [TEX][n_P,u_d][/TEX]
d' nằm trong (P) nên d' vuông góc với vtpt [TEX]n_P[/TEX]
Vậy kết quả cuối cùng thu được: [TEX]u_{d'}=[[n_P;u_d];n_P][/TEX]
Có vtcp, có điểm đi qua ( là A) , ta có thể viết được pt của d' rồi.
Trên đây là 1 số dạng nhỏ, tất nhiên đề bài có thể biến tấu đi, chúng ta phải tưởng tượng một chút để có thể vẽ hình và tìm ra hướng giải!
