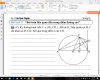
Đây đều là những dạng quen thuộc của các dạng của đường tròn euler:
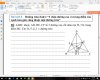
Câu 10:
a) Bạn chứng minh $HBKC$ là hbh.
Do đó 2 đường chéo cắt nhau tại trung điểm mỗi đường. Do đó $H,M,K$ thẳng hàng.
b)$O,M$ là trung điểm của $AK,HK$ nên nó là đường trung bình
c) Chứng minh $AHOO'$ là hbh thì sử dụng tính chất 2 cặp cạnh đối song song là ok. (Lưu ý vuông góc)
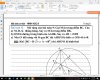
Câu 14:
$F$ là trung điểm nên $OF \perp DE$.
Từ đó dễ dàng cm đc: $A,B,O,C$ cùng thuộc một đường tròn và $A,B,O,F$ cùng thuộc một đường tròn.
Do đó 5 điểm $A,B,O,F,C$ cùng thuộc một đường tròn.
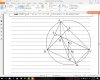
Câu 15:
Bạn chứng minh $\triangle MKI \sim \triangle MIH$ theo trường hợp (g.g) bằng cách xài tgnt.
Nên sẽ suy ra được: $MI^2=MH.MK$.
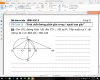
câu 16:
bạn chứng minh: $OC$ là phân giác góc $ACB$(Xài các góc nội tiếp góc tạo bởi t/t dây cung) mà $OC \perp MC$ nên $MC$ là phân giác góc ngoài.
áp dụng t/c phân giác trong, ngoài ta có ngay dpcm
câu 17:
Câu này có rất nhiều cách nhưng cách mình thường dùng là:
Kẻ tiếp tuyến tại $A$ cắt $CD$ tại $K$.
Sau đó áp dụng tales cho $IH//DB$ và $CI//KA$ kết hợp t/c tiếp tuyến thì ta sẽ có $IC=IH$.
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Bài 9 mình làm được rồi còn bài 10 chưa nha
