Vật lí 10 mô men lực

[Elishuchi]

[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Chắc suất Đại học top - Giữ chỗ ngay!!

ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.

mọi người vẽ véc tơ lực chiếu hình và làm cụ thể mình với

 

[Deathheart]

View attachment 160775
mọi người vẽ véc tơ lực chiếu hình và làm cụ thể mình với

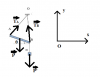
Chọn hệ trục Oxy như hình vẽ. Để hệ cân bằng thì:
$$\vec{T_A}+\vec{T_B}+\vec{P}+\vec{P'}=\vec{0}$$
Chiếu lên phương Ox:
$$T_A.cos(60^0-\theta)-T_{B}.sin(30^0-\theta)=0$$
$$\Rightarrow T_A.cos(60^0-\theta).cos(30^0-\theta)-T_{B}.sin(30^0-\theta)cos(30^0-\theta)=0$$ (1)
Chiếu lên phương Oy:
$$T_A.sin(60^0-\theta)+T_B.cos(30^0-\theta)-2mg=0$$
$$\Rightarrow T_A.sin(60^0-\theta).sin(30^0-\theta)+T_B.cos(30^0-\theta).sin(30^0-\theta)-2mg.sin(30^0-\theta)=0$$ (2)
Chọn trục quay tại B, hệ đứng yên nên:
$$\frac{1}{2}mgL.cos\theta-T_AL.sin60^0=0\Leftrightarrow \frac{1}{2}mgL.cos\theta=T_AL.sin60^0$$$$\Rightarrow \frac{1}{2}mg.cos\theta=T_A.sin60^0$$ (3)
Lấy (1) cộng với (2) suy ra: $$T_A.cos30^0=2mg.sin(30^0-\theta)$$ (4)
Lấy (4) chia (3) ta được: $$1=4.\frac{sin(30^0-\theta)}{cos\theta}\Rightarrow \theta\approx 16^06'$$

Có $$\theta$$ rồi thì thay vào (4) và (1) là ra $$T_A$$ và $$T_B$$ thôi