- 27 Tháng mười 2018
- 3,742
- 3,706
- 561
- Hà Nội
- Trường Đại học Bách Khoa Hà Nội
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Đặt vấn đề: Nếu đi thi các bạn gặp những bài như thế này thì sao?

Khi mà chúng ta không phải là những người có khả năng biến đổi và tính toán siêu đẳng. Thì vẫn sẽ có cách để ta tính được những bài dạng thế này, bằng dùng máy tính. Với dạng câu này xuất hiện thì cũng đánh giá nó nằm ở ngưỡng 8 điểm rồi, nên dẫu mẹo casio cũng không phải một phát mà ăn ngay. Chúng ta phải suy nghĩ một chút, nhưng đương nhiên dễ hơn rất nhiều so với giải tay bình thường rồi.
Tất cả những bài dạng tổng dãy quy luật, tuy bấm máy có thể không ra được đáp án ( hoặc rất lâu mới ra), nhưng ta có thể "thử với giá trị nhỏ" , tức là giá trị mà máy tính được nhanh gọn. Sau đấy ta sẽ nhìn 4 đáp án để đoán ra quy luật tương ứng. Và tổng quy luật này trong máy tính có thể sử dụng : tổng sigma [tex]\sum_{}^{}[/tex]
Cái tổng sigma chắc ai cũng biết rồi, ví dụ [tex]\sum_{k=1}^{10}x^2[/tex], thì nó cứ nhằm chỗ nào có x mà thay k tương ứng vào đấy . Ở đây k chạy từ 1 đến 10 nên nó cứ thay k lần lượt từ 1 đến 10, rồi cộng tất cả các giá trị lại với nhau. Và khác mới mode 7 table của máy, bạn có thể tùy ý chọn step, thì ở tổng sigma này, step chỉ có thể nhảy từng 1 đơn vị.
Vì vậy tùy từng bài toán mà ta phải suy nghĩ biến đổi tương ứng sao cho step đúng.
Trở lại bài toán nêu trên. Là 1 bài tổng theo quy luật, tuy nhiên rõ ràng step của nó là [tex]\frac{1}{2019}[/tex], là phân số chứ không phải là từng 1 đơn vị. Vậy ta phải biến đổi sao cho khi "k" nhảy 1 đơn vị thì nó vẫn đúng. Rất đơn giản ta nhập như sau :

Dưới mẫu bị khuất đi nhưng nó tương tự trên tử nên chắc các bạn cũng đoán được. Nếu ai không tin thì cứ thay thử từng x từ 1 trở đi sẽ thấy nó đúng như biểu thức ta cần tính. Đây chính là " 1 chút phải suy nghĩ " mà mình đã đề cập ở trên.
Đến đây chỉ cần ấn "=" có thể ra 1009, tuy nhiên, dù số là nhỏ. Nhưng máy tính rất lâu, ở giả lập CPU rất nhanh nhưng mình cũng mất vài phút. Vậy cách tối ưu hơn là ta thử với giá trị nhỏ. Để đoán quy luật.
Ta chỉ cần chọn x nhỏ như x=19 chẳng hạn. (phải chọn số lẻ tương tự như đề họ cho, nếu ở đề là 2020 thì chọn 20, vì chẵn lẻ khác nhau dẫn đến kết quả theo quy luật cũng khác nhau )
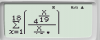
nhanh gọn có kết quả:

Dựa vào 4 đáp án sẽ dễ dàng nhận ra A là đáp án, vì nó đều cùng 1 kiểu x-1)/2 , cụ thể ( 2019-1)/2 = 1009, (19-1)/2=9
x-1)/2 , cụ thể ( 2019-1)/2 = 1009, (19-1)/2=9
Tổng kết lại, có 2 bước ta phải suy nghĩ 1 tí, đó là : biến đổi để nhập liệu cho đúng , và chọn số nhỏ để đoán quy luật của kết quả.
Ví dụ 2: Tínhtổng [tex]S=1^2C_{2019}^{1}2^{2008}+2^2C_{2009}^{2}.2^{2007}+3^2.C_{2009}^{3}.2^{2006}+...+2009^2.C_{2009}^{2009}[/tex] .
A. [TEX]2011.2009.3^{2007}[/TEX]
B. [TEX]2010.2012.3^{2009}[/TEX]
C. [TEX]2011.2009.3^{2009}[/TEX]
D. [TEX]2011.2013.3^{2011}[/TEX]
Bài này thì xem cả 4 kết quả rõ ràng vượt xa khả năng tính của máy. Đương nhiên ta phải dùng đến thử số nhỏ rồi.
Xem xét quy luật , với từng số hạng, ví dụ [TEX]1^2C_{2019}^{1}2^{2008}[/TEX]
Thì [TEX]1^2[/TEX] sẽ bắt đầu tăng dần 1 đơn vị sau mỗi số hạng : [TEX]2^2,3^2[/TEX]
[TEX]C_{2019}^{1}[/TEX] cũng bắt đầu tăng dần k lên 1 đơn vị
[TEX]2^{2008}[/TEX] thì số mũ giảm dần 1, vậy tổng quát bấm máy:
[tex]\sum_{1}^{2009}x^2.C_{2009}^{x}.2^{2009-x}[/tex]
Chọn số nhỏ, thử với 9 thôi là được:
[tex]\sum_{1}^{9}x^2.C_{9}^{x}.2^{9-x}[/tex]
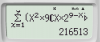
Bắt đầu xem với đáp án A. Khi ánh xạ tương ứng sang thử số nhỏ, cụ thể là 9, ta sẽ thấy nó là [TEX]11.9.3^7[/TEX]
Bấm máy có [TEX]11.9.3^7=216513[/TEX]
Vậy A là đáp án luôn
Tóm lại dạng tính tổng này bài nào cũng dùng Casio được. Các bạn có thể luyện tập với các bài khác. Nếu có bài nào dạng này mà không tìm ra được, các bạn có thể hỏi vào đây
Khi mà chúng ta không phải là những người có khả năng biến đổi và tính toán siêu đẳng. Thì vẫn sẽ có cách để ta tính được những bài dạng thế này, bằng dùng máy tính. Với dạng câu này xuất hiện thì cũng đánh giá nó nằm ở ngưỡng 8 điểm rồi, nên dẫu mẹo casio cũng không phải một phát mà ăn ngay. Chúng ta phải suy nghĩ một chút, nhưng đương nhiên dễ hơn rất nhiều so với giải tay bình thường rồi.
Tất cả những bài dạng tổng dãy quy luật, tuy bấm máy có thể không ra được đáp án ( hoặc rất lâu mới ra), nhưng ta có thể "thử với giá trị nhỏ" , tức là giá trị mà máy tính được nhanh gọn. Sau đấy ta sẽ nhìn 4 đáp án để đoán ra quy luật tương ứng. Và tổng quy luật này trong máy tính có thể sử dụng : tổng sigma [tex]\sum_{}^{}[/tex]
Cái tổng sigma chắc ai cũng biết rồi, ví dụ [tex]\sum_{k=1}^{10}x^2[/tex], thì nó cứ nhằm chỗ nào có x mà thay k tương ứng vào đấy . Ở đây k chạy từ 1 đến 10 nên nó cứ thay k lần lượt từ 1 đến 10, rồi cộng tất cả các giá trị lại với nhau. Và khác mới mode 7 table của máy, bạn có thể tùy ý chọn step, thì ở tổng sigma này, step chỉ có thể nhảy từng 1 đơn vị.
Vì vậy tùy từng bài toán mà ta phải suy nghĩ biến đổi tương ứng sao cho step đúng.
Trở lại bài toán nêu trên. Là 1 bài tổng theo quy luật, tuy nhiên rõ ràng step của nó là [tex]\frac{1}{2019}[/tex], là phân số chứ không phải là từng 1 đơn vị. Vậy ta phải biến đổi sao cho khi "k" nhảy 1 đơn vị thì nó vẫn đúng. Rất đơn giản ta nhập như sau :
Dưới mẫu bị khuất đi nhưng nó tương tự trên tử nên chắc các bạn cũng đoán được. Nếu ai không tin thì cứ thay thử từng x từ 1 trở đi sẽ thấy nó đúng như biểu thức ta cần tính. Đây chính là " 1 chút phải suy nghĩ " mà mình đã đề cập ở trên.
Đến đây chỉ cần ấn "=" có thể ra 1009, tuy nhiên, dù số là nhỏ. Nhưng máy tính rất lâu, ở giả lập CPU rất nhanh nhưng mình cũng mất vài phút. Vậy cách tối ưu hơn là ta thử với giá trị nhỏ. Để đoán quy luật.
Ta chỉ cần chọn x nhỏ như x=19 chẳng hạn. (phải chọn số lẻ tương tự như đề họ cho, nếu ở đề là 2020 thì chọn 20, vì chẵn lẻ khác nhau dẫn đến kết quả theo quy luật cũng khác nhau )
nhanh gọn có kết quả:
Dựa vào 4 đáp án sẽ dễ dàng nhận ra A là đáp án, vì nó đều cùng 1 kiểu
Tổng kết lại, có 2 bước ta phải suy nghĩ 1 tí, đó là : biến đổi để nhập liệu cho đúng , và chọn số nhỏ để đoán quy luật của kết quả.
Ví dụ 2: Tínhtổng [tex]S=1^2C_{2019}^{1}2^{2008}+2^2C_{2009}^{2}.2^{2007}+3^2.C_{2009}^{3}.2^{2006}+...+2009^2.C_{2009}^{2009}[/tex] .
A. [TEX]2011.2009.3^{2007}[/TEX]
B. [TEX]2010.2012.3^{2009}[/TEX]
C. [TEX]2011.2009.3^{2009}[/TEX]
D. [TEX]2011.2013.3^{2011}[/TEX]
Bài này thì xem cả 4 kết quả rõ ràng vượt xa khả năng tính của máy. Đương nhiên ta phải dùng đến thử số nhỏ rồi.
Xem xét quy luật , với từng số hạng, ví dụ [TEX]1^2C_{2019}^{1}2^{2008}[/TEX]
Thì [TEX]1^2[/TEX] sẽ bắt đầu tăng dần 1 đơn vị sau mỗi số hạng : [TEX]2^2,3^2[/TEX]
[TEX]C_{2019}^{1}[/TEX] cũng bắt đầu tăng dần k lên 1 đơn vị
[TEX]2^{2008}[/TEX] thì số mũ giảm dần 1, vậy tổng quát bấm máy:
[tex]\sum_{1}^{2009}x^2.C_{2009}^{x}.2^{2009-x}[/tex]
Chọn số nhỏ, thử với 9 thôi là được:
[tex]\sum_{1}^{9}x^2.C_{9}^{x}.2^{9-x}[/tex]
Bắt đầu xem với đáp án A. Khi ánh xạ tương ứng sang thử số nhỏ, cụ thể là 9, ta sẽ thấy nó là [TEX]11.9.3^7[/TEX]
Bấm máy có [TEX]11.9.3^7=216513[/TEX]
Vậy A là đáp án luôn
Tóm lại dạng tính tổng này bài nào cũng dùng Casio được. Các bạn có thể luyện tập với các bài khác. Nếu có bài nào dạng này mà không tìm ra được, các bạn có thể hỏi vào đây

