[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
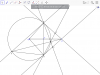
cho OM=3R (điểm M nằm ngoài đường tròn ).Vẽ MA,MB là hai tiếp tuyến .vẽ AD//MB ,MD cắt (O) tại C,BC cắt MA tại F , AC cắt MB tại E.
1)Cm MAOB nội tiếp
2)Cm [tex]EB^2=EC.EA[/tex]
3)Cm E là trung điểm MB
4)Cm [tex]BC.BM=MC.AB[/tex]
5)Cm tia CF là phân giác của góc MCA
6)Tính diện tích tam giác ABD theo R
1)Cm MAOB nội tiếp
2)Cm [tex]EB^2=EC.EA[/tex]
3)Cm E là trung điểm MB
4)Cm [tex]BC.BM=MC.AB[/tex]
5)Cm tia CF là phân giác của góc MCA
6)Tính diện tích tam giác ABD theo R