- 20 Tháng chín 2013
- 5,018
- 7,484
- 941
- TP Hồ Chí Minh
- Đại học Bách Khoa TPHCM
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chào các bạn  Mình xin phép mở đầu bài viết bằng một bài toán hình học:
Mình xin phép mở đầu bài viết bằng một bài toán hình học:
Có thể nói, hình học THCS chỉ bao gồm những thành phần cơ bản là cạnh và góc. Tuy vậy, khi những yếu tố đơn giản đó kết hợp lại với nhau, chúng tạo nên những kết quả hết sức bất ngờ và thú vị:
Khi bạn bắt đầu học hình học, bạn sẽ bắt đầu hỏi: làm thế nào để chứng minh các điểm thẳng hàng, các đường thẳng đồng quy, làm thế nào để abcxyz... Nhưng càng trải qua nhiều bài toán, bạn sẽ tự nhận ra là: không có một cách hay phương pháp cố định nào để chứng minh cả! Vậy làm thế nào...???
Mỗi người sẽ có một câu trả lời khác nhau cho vấn đề này. Với mình, đó là sự khác biệt giữa một học sinh bình thường học hình học và một học sinh giỏi học hình học. Một học sinh giỏi không đơn thuần chỉ dựa vào phương pháp để làm bài, mà còn dựa trên kinh nghiệm của hàng chục, hàng trăm bài toán mà bạn ấy đã đi qua để nhờ đó mà giải một bài toán mới!
Topic này sẽ cung cấp cho các bạn một số bài tập trong các đề thi gần đây để rèn luyện kinh nghiệm của mình. Ngoài ra, mình sẽ cung cấp các bạn một số kiến thức cơ bản, một số phương pháp, cũng như một số kinh nghiệm của mình trong việc giải các bài toán hình học.
Cùng bắt đầu nhé!
Tổng hợp kiến thức
Lưu ý: Những định lý được dùng
Các bạn lưu ý, trong quá trình học hình học, bạn sẽ gặp phải một số định lý mới. Mình sẽ điểm tên một số:
Trong khuôn khổ topic thì mình sẽ chỉ dùng đến kiến thức lớp 7, lớp 8, lớp 9, ngoại trừ một số trường hợp đặc biệt như phương tích.
Kiến thức lớp 7
Bao gồm những kiến thức chưa liên quan đến tỉ lệ mà chỉ thông qua biến đổi dấu bằng:
Bao gồm những kiến thức liên quan đến tỉ lệ:
Bao gồm những kiến thức liên quan đến đường tròn và tứ giác nội tiếp.
Mình sẽ nhóm các kiến thức theo chủ đề, thay vì nhóm theo lớp nhé.
Tứ giác nội tiếp
Các tính chất về góc trong đường tròn
Giả sử ta có hình như hình vẽ. Khi đó ta có các hệ thức:
Tính chất 3, bạn có thể chứng minh như sau:
Với tứ giác nội tiếp như hình vẽ, bạn sẽ có các tính chất như sau:
Tính chất về cạnh trong tứ giác nội tiếp (phương tích)
Trong tứ giác nội tiếp, có một tính chất khá là hữu ích như sau:
Tính chất này bạn dùng bằng cách chứng minh lại bằng tam giác đồng dạng và biến đổi cạnh nhé.
Những kiến thức trên cũng chưa hẳn là phần "HSG" đâu. Phần HSG, như mình nói lúc trước, là những kỹ thuật bạn sử dụng để giải bài toán, dựa trên những kiến thức nền tảng trên. Mình xin trình bày một số kỹ thuật mà mình biết (mình không biết chính xác tên gọi, nhưng nếu được, bạn hãy đọc tiếp để hiểu ý tưởng nha):
Ngàymai mốt mình sẽ đăng topic bài tập, các bạn đón chờ nhé 
- Ở hình học lớp 7, các bạn học về đường thẳng song song, tam giác bằng nhau, ... Đây là những kiến thức nền tảng để biến đổi những thứ bằng nhau, đặc biệt là góc.
- Ở hình học lớp 8, các bạn học về định lý Ta-lét, tam giác đồng dạng. Đây là những kiến thức nền tảng để biến đổi những thứ tỉ lệ nhau, đặc biệt là cạnh.
- Ở hình học lớp 9, các bạn học về đường tròn. Đường tròn là thứ khó nhất trong chương trình: bạn sẽ không biết là mình cần sử dụng yếu tố cạnh hay yếu tố góc để giải quyết bài toán nữa! Nhờ đó, đây cũng là chủ đề chính trong chương trình HSG Toán THCS!
"There is no royal road to geometry" - Euclid
Khi bạn bắt đầu học hình học, bạn sẽ bắt đầu hỏi: làm thế nào để chứng minh các điểm thẳng hàng, các đường thẳng đồng quy, làm thế nào để abcxyz... Nhưng càng trải qua nhiều bài toán, bạn sẽ tự nhận ra là: không có một cách hay phương pháp cố định nào để chứng minh cả! Vậy làm thế nào...???
Mỗi người sẽ có một câu trả lời khác nhau cho vấn đề này. Với mình, đó là sự khác biệt giữa một học sinh bình thường học hình học và một học sinh giỏi học hình học. Một học sinh giỏi không đơn thuần chỉ dựa vào phương pháp để làm bài, mà còn dựa trên kinh nghiệm của hàng chục, hàng trăm bài toán mà bạn ấy đã đi qua để nhờ đó mà giải một bài toán mới!
Topic này sẽ cung cấp cho các bạn một số bài tập trong các đề thi gần đây để rèn luyện kinh nghiệm của mình. Ngoài ra, mình sẽ cung cấp các bạn một số kiến thức cơ bản, một số phương pháp, cũng như một số kinh nghiệm của mình trong việc giải các bài toán hình học.
Cùng bắt đầu nhé!
Tổng hợp kiến thức
Lưu ý: Những định lý được dùng
Các bạn lưu ý, trong quá trình học hình học, bạn sẽ gặp phải một số định lý mới. Mình sẽ điểm tên một số:
- Định lý Ceva, Menelaus (Me-ne-le-uýt) về cách xử lý đồng quy, thẳng hàng
- Định lý Ptolemy (Ptô-lê-mê) về mối liên hệ giữa các cạnh trong tứ giác nội tiếp
- Kiến thức về phương tích, trục đẳng phương trong đường tròn
- ...
Trong khuôn khổ topic thì mình sẽ chỉ dùng đến kiến thức lớp 7, lớp 8, lớp 9, ngoại trừ một số trường hợp đặc biệt như phương tích.
Kiến thức lớp 7
Bao gồm những kiến thức chưa liên quan đến tỉ lệ mà chỉ thông qua biến đổi dấu bằng:
- Định lý Pytago
- Tam giác bằng nhau
- Tính chất về tâm đường tròn bàng tiếp
Bao gồm những kiến thức liên quan đến tỉ lệ:
- Định lý Ta-lét
- Tam giác đồng dạng
- Định lý đường phân giác
Bao gồm những kiến thức liên quan đến đường tròn và tứ giác nội tiếp.
Mình sẽ nhóm các kiến thức theo chủ đề, thay vì nhóm theo lớp nhé.
Tứ giác nội tiếp
Các tính chất về góc trong đường tròn
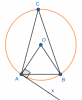
Giả sử ta có hình như hình vẽ. Khi đó ta có các hệ thức:
- $\widehat{AOB} = 2 \widehat{ACB}$: góc ở tâm gấp đôi góc nội tiếp
- $\widehat{xAB} = \widehat{ACB}$: góc tạo bởi tia tiếp tuyến và dây cung bằng góc nội tiếp
- $\widehat{OBA} = 90^\circ - \widehat{ACB}$: tính chất này không có trong SGK
Tính chất 3, bạn có thể chứng minh như sau:
- $\widehat{OBA} = 90^\circ - \dfrac12 \widehat{AOB} = 90^\circ - \widehat{ACB}$ (do $\triangle{OAB}$ cân tại $O$ và tính chất góc ở tâm)
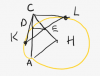
Với tứ giác nội tiếp như hình vẽ, bạn sẽ có các tính chất như sau:
- $\widehat{DAC} = \widehat{DBC}$: góc nội tiếp chắn cung $DC$
- $\widehat{JAB} = \widehat{BCD}$: tính chất góc ngoài tứ giác nội tiếp
- $\widehat{ABC} + \widehat{ADC} = 180^\circ$: tính chất tổng hai góc đối tứ giác nội tiếp
Tính chất về cạnh trong tứ giác nội tiếp (phương tích)
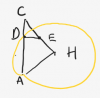
Trong tứ giác nội tiếp, có một tính chất khá là hữu ích như sau:
- $IA \cdot IC = IB \cdot ID = R^2 - IO^2$
- $JA \cdot JD = JB \cdot JC = JO^2 - R^2$
Tính chất này bạn dùng bằng cách chứng minh lại bằng tam giác đồng dạng và biến đổi cạnh nhé.
Những kiến thức trên cũng chưa hẳn là phần "HSG" đâu. Phần HSG, như mình nói lúc trước, là những kỹ thuật bạn sử dụng để giải bài toán, dựa trên những kiến thức nền tảng trên. Mình xin trình bày một số kỹ thuật mà mình biết (mình không biết chính xác tên gọi, nhưng nếu được, bạn hãy đọc tiếp để hiểu ý tưởng nha):
- Biến đổi góc ("đuổi góc", angle chasing)
- Biến đổi tỉ lệ
- Điểm duy nhất (điểm trùng, ...)
- Đổi mô hình
- ...
Ngày