[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
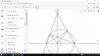
cho đường tròn tâm O đường kính AB .2 dây cung AC,BD cắt nhau ở H. 2 tia AD,BC cắt nhau ở K
CM a, 4 điểm K,D,H,C thuộc 1 đường tròn
b, KH cắt AB ở I. CM: IH là phân giác [tex]\widehat{DIC}[/tex]
c, Tìm vị trí của C và D để IH.IK đạt giá trị lớn nhất
CM a, 4 điểm K,D,H,C thuộc 1 đường tròn
b, KH cắt AB ở I. CM: IH là phân giác [tex]\widehat{DIC}[/tex]
c, Tìm vị trí của C và D để IH.IK đạt giá trị lớn nhất