[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
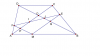
Qua một điểm M tùy ý đã cho trên đáy lớn AB của hình thang ABCD ta kẻ các đường thẳng song song với 2 đường chéo AC và BD. Các đường thẳng song song này cắt 2 cạnh BC và AD lần lượt tại E và F. Đoạn EF cắt AC và BD tại I và J tương ứng.
a) Chứng minh rằng nếu H là trung điểm của Ị thì H cũng là trung điểm của EF
b) Trong trường hợp AB=2CD, hãy chỉ ra vị trí của 1 điểm M trên AB sao cho EJ=JI=IF.
a) Chứng minh rằng nếu H là trung điểm của Ị thì H cũng là trung điểm của EF
b) Trong trường hợp AB=2CD, hãy chỉ ra vị trí của 1 điểm M trên AB sao cho EJ=JI=IF.