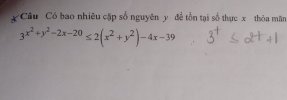Các bạn giúp mình bài này được không
Nguyễn Đặng Lan Anh
Đặt [imath]t=x^2+y^2-2x-20[/imath]
bpt [imath]\Leftrightarrow 3^t\le 2t+1[/imath]
Xét [imath]f(t)=3^t-2t-1[/imath]
[imath]f'(t)=3^t\ln 3-2[/imath]
[imath]f'(t)=0\iff t=\log_3 \left(\dfrac{2}{\ln3}\right)[/imath]
Dựa vào bbt ta có [imath]f(t)=0[/imath] có 2 ngiệm
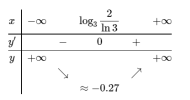
mà [imath]f(0)=f(1)=0[/imath]
suy ra [imath]f(t)\le 0\Leftrightarrow 0\le t\le 1[/imath]
[imath]\Rightarrow 0\le x^2+y^2-2x-20\le 1[/imath]
[imath]\Rightarrow 21-y^2\le (x-1)^2\le 22-y^2[/imath]
Để tồn tại x thì [imath]22-y^2\ge 0\Rightarrow y\in [-4;4][/imath]
Có gì khúc mắc em hỏi lại nhé
Ngoài ra em xem thêm tại
Chinh phục kì thi THPTQG môn Toán 2022
 [TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.