mn giải chi tiết giúp mik bài này vs
leduymanh2005
a/
- Tốc độ m ngay trước khi va chạm:
vật m rơi tự do từ độ cao h so với M, thời gian rơi là: [imath]h=\frac{1}{2}gt^2=>t=\frac{\sqrt[]{3}}{20}s[/imath] (chú ý đổi h về đơn vị mét)
Tốc độ m ngay trước va chạm: [imath]v=g.t=\frac{\sqrt[]{3}}{2}m/s[/imath]
- Tốc độ 2 vật sau va chạm:
Bảo toàn động lượng trước và sau va chạm:
[imath]m.v=(m+M).v'=>v'=\frac{\sqrt[]{3}}{5}m/s[/imath]
b/
Sau va chạm, m,M dính vào nhau cùng dao động điều hòa vì thế vị trí cân bằng sẽ thấp hơn vị trí cân bằng cũ của M trước va chạm 1 đoạn là:
[imath]\Delta l=\frac{(m+M)g}{k}-\frac{Mg}{k}=\frac{mg}{k}=0,01m[/imath]
Biên độ dao động:
[imath](\Delta l)^2+\frac{v'^2}{w^2}=(\Delta l)^2+\frac{v'^2}{\frac{k}{m+M}}=A^2=>A=0,02m[/imath]
Dùng đường tròn xác định pha ban đầu:
t=0 vật qua vị trí [imath]x=\frac{A}{2}[/imath] và theo chiều âm (do chọn trục Ox hướng lên mà vật đi xuống) nên điểm pha Po như hình
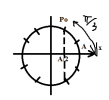
Phương trình dao động: [imath]x=Acos(wt+\varphi)-\Delta l=Acos(\sqrt[]{\frac{k}{m+M}}t+\varphi)-\Delta l=0,02cos(20t+\frac{\pi}{3})-0,01(m)[/imath]
c/ Tốc độ trung bình từ lúc va chạm(t=0) đến khi lên đến độ cao cực đại (Biên dương) lần thứ nhất:
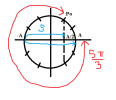
Từ đường tròn, dễ thấy quãng đường vật di chuyển:
[imath]S=\frac{A}{2}+A+A+A=3,5A=3,5.0,02=0,07m[/imath]
Thời gian đi:
[imath]\Delta t=\frac{\frac{5\pi}{3}}{w}=\frac{\pi}{12}s[/imath]
Tốc độ trung bình là:
[imath]Vtb=\frac{S}{\Delta t}=0,267 m/s[/imath]
d/
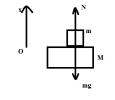
Định luật II Newton đối với m:
[imath]N-mg=ma=>N=m(g+a)=m(g-w^2.x)=m(g-w^2.A.cos(wt+\varphi))[/imath]
Để m không rời M, luôn dính với M khi dao động thì:
[imath]N \ge 0=>m(g-w^2.A.cos(wt+\varphi)) \ge0=>g-w^2.A.cos(wt+\varphi)\ge 0[/imath]
Đặt [imath]y=g-w^2.A.cos(wt+\varphi) \ge0[/imath] suy ra [imath]Miny \ge0=>g - w^2A \ge 0 =>\frac{g}{w^2} \ge A=>A\le 0,025 m[/imath]
Chúc bạn học tốt!
-----------
Xem thêm:
Kĩ thuật dùng đường tròn để giải những bài dao động cơ 
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
Hocmai Forum 