[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
[TẶNG BẠN] TRỌN BỘ Bí kíp học tốt 08 môn
 Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
Chắc suất Đại học top - Giữ chỗ ngay!!
ĐĂNG BÀI NGAY để cùng trao đổi với các thành viên siêu nhiệt tình & dễ thương trên diễn đàn.
mn giúp mình bài này vs ạ , mình đang cần gấp , mình cảm ơn nhiều ạ.
Hai vật thực hiện dao động điều hòa cùng phương, cùng tần số trên trục Ox với biên độ [tex]A_1 = 3cm, A_2 = 6cm[/tex]. Biết tích li độ của hai vật theo thời gian được biểu diễn như hình vẽ. Khoảng cách xa nhất của hai vật trong quá trình dao động có giá trị gần nhất:
A. 8cm B. 7cm
C. 9cm D. 5cm
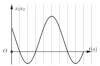
Hai vật thực hiện dao động điều hòa cùng phương, cùng tần số trên trục Ox với biên độ [tex]A_1 = 3cm, A_2 = 6cm[/tex]. Biết tích li độ của hai vật theo thời gian được biểu diễn như hình vẽ. Khoảng cách xa nhất của hai vật trong quá trình dao động có giá trị gần nhất:
A. 8cm B. 7cm
C. 9cm D. 5cm